Bạn đã bao giờ tự hỏi về những con số mình gặp hàng ngày chưa? Khi xem dự báo thời tiết, thấy nhiệt độ có lúc 10°C, có lúc lại -2°C. Khi quản lý chi tiêu, có lúc bạn có thêm tiền (dương), có lúc lại nợ (âm). Hay đơn giản là khi đếm số tầng trong thang máy, có tầng 1, 2, 3… nhưng cũng có tầng hầm B1, B2… Những con số “âm”, “dương” và cả số 0 đặc biệt đó chính là thành viên của một gia đình lớn trong toán học – gia đình Số Nguyên.
Nghe quen thuộc đúng không? Nhưng liệu bạn đã thực sự hiểu rõ về “người bạn” này chưa? Tại sao chúng lại quan trọng và xuất hiện khắp mọi nơi như vậy? Cùng Tài Liệu Siêu Cấp khám phá tất tần tật về Số Nguyên trong bài viết này nhé! Đảm bảo sau khi đọc xong, bạn sẽ thấy chúng không chỉ là những con số khô khan đâu!
Số Nguyên Là Gì? Một Khái Niệm Căn Bản Không Thể Bỏ Qua
Chắc hẳn bạn đã quá quen với các số tự nhiên dùng để đếm: 1, 2, 3, 4,… phải không nào? Nhưng cuộc sống đâu chỉ có “thêm vào” và “đếm tới”. Đôi khi chúng ta cần biểu thị sự thiếu hụt, sự giảm sút, hay những giá trị dưới mức 0. Đó chính là lúc số nguyên xuất hiện như một vị cứu tinh!
Vậy số nguyên là gì?
Nói một cách dễ hiểu, số nguyên bao gồm:
- Số nguyên dương: Chính là các số tự nhiên lớn hơn 0 (1, 2, 3, …). Chúng biểu thị sự tăng lên, có thêm, hoặc giá trị trên mức chuẩn.
- Số nguyên âm: Là các số đối của số nguyên dương (-1, -2, -3, …). Chúng biểu thị sự giảm đi, nợ nần, hoặc giá trị dưới mức chuẩn.
- Số 0: Một con số đặc biệt, không phải là số nguyên dương cũng không phải số nguyên âm. Nó là điểm gốc, điểm cân bằng.
Tập hợp số nguyên – Ngôi nhà chung ký hiệu là Z
Trong toán học, người ta dùng ký hiệu Z (xuất phát từ “Zahlen” trong tiếng Đức, nghĩa là “số”) để biểu thị tập hợp tất cả các số nguyên.
Vậy, Z = {…, -3, -2, -1, 0, 1, 2, 3, …}
Tập hợp này kéo dài vô tận về cả hai phía âm và dương. Thật là một gia đình đông đúc và thú vị!
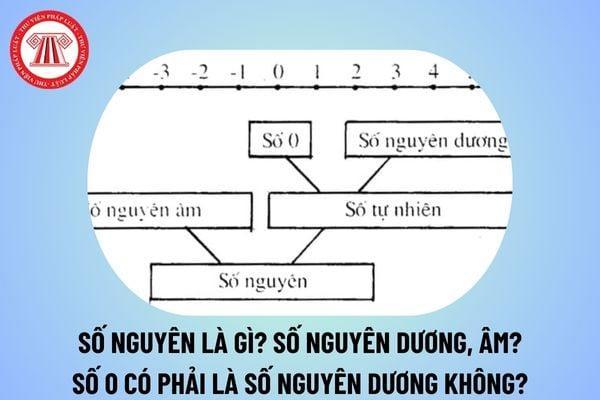 Tập hợp số nguyên Z bao gồm số nguyên âm, số 0 và số nguyên dương
Tập hợp số nguyên Z bao gồm số nguyên âm, số 0 và số nguyên dương
Caption: Tập hợp Z – Ngôi nhà chung của tất cả các số nguyên, từ âm vô cùng đến dương vô cùng.
Khám Phá Các Thành Viên Trong Gia Đình Số Nguyên
Mỗi thành viên trong gia đình số nguyên đều có vai trò và đặc điểm riêng. Cùng làm quen kỹ hơn nhé!
Số nguyên dương: Những người bạn “luôn tiến về phía trước”
Đây chính là các số tự nhiên mà chúng ta dùng để đếm hàng ngày: 1, 2, 3, 100, 1000,… Chúng luôn mang giá trị lớn hơn 0. Khi bạn có thêm 5 cái kẹo, bạn đang làm việc với số nguyên dương +5. Khi nhiệt độ là 25°C, đó là một giá trị dương.
Số nguyên âm: Thế giới “dưới mực không”
Số nguyên âm là những số nhỏ hơn 0: -1, -2, -3, -50, -200,… Chúng thường được dùng để biểu thị sự thiếu hụt, nợ nần, hoặc giá trị dưới một mức chuẩn nào đó.
- Bạn nợ bạn bè 50.000 VNĐ? Có thể biểu thị là -50.000.
- Nhiệt độ ngoài trời là -5°C? Rất lạnh!
- Bạn đang ở tầng hầm B2 của tòa nhà? Đó là tầng -2 so với mặt đất.
Số 0: Điểm cân bằng đặc biệt
Số 0 là một thành viên vô cùng quan trọng. Nó không dương cũng không âm. Số 0 đóng vai trò là gốc, là ranh giới giữa phần dương và phần âm. Nó cũng có những tính chất đặc biệt trong các phép toán (ví dụ: bất kỳ số nào cộng với 0 đều bằng chính nó, bất kỳ số nào nhân với 0 đều bằng 0).
Câu hỏi thường gặp: Số 0 có phải là số nguyên không?
Trả lời: Chắc chắn rồi! Số 0 là một thành viên không thể thiếu của tập hợp số nguyên Z.
Câu hỏi thường gặp: Số thập phân (ví dụ: 1.5) hoặc phân số (ví dụ: 1/2) có phải là số nguyên không?
Trả lời: Không. Số nguyên là các số toàn vẹn, không có phần lẻ thập phân. 1.5 hay 1/2 không thuộc tập hợp Z.
Biểu Diễn Số Nguyên Trên Trục Số: Trực Quan Hóa Khái Niệm
Bạn thấy khó hình dung về số âm? Đừng lo, có một công cụ cực kỳ hữu ích: Trục số.
Hãy tưởng tượng một đường thẳng nằm ngang:
- Ở giữa là điểm gốc, biểu thị số 0.
- Bên phải số 0 là các số nguyên dương, tăng dần từ phải sang trái (1, 2, 3,…).
- Bên trái số 0 là các số nguyên âm, giảm dần từ trái sang phải (-1, -2, -3,…).
 Trục số biểu diễn các số nguyên âm, số 0 và số nguyên dương
Trục số biểu diễn các số nguyên âm, số 0 và số nguyên dương
Caption: Trục số – Công cụ trực quan giúp bạn dễ dàng hình dung vị trí và mối quan hệ giữa các số nguyên.
Nhìn vào trục số, bạn có thể thấy ngay:
- Số bên phải luôn lớn hơn số bên trái (ví dụ: 3 > 1, 1 > 0, 0 > -2, -2 > -5).
- Hai số đối nhau (như 3 và -3) cách đều điểm 0.
Các Phép Toán Cơ Bản Với Số Nguyên: Xây Dựng Nền Tảng Toán Học
Giống như số tự nhiên, chúng ta hoàn toàn có thể thực hiện các phép cộng, trừ, nhân, chia với số nguyên. Tuy nhiên, sự xuất hiện của số âm sẽ mang đến một vài quy tắc thú vị cần ghi nhớ.
Cộng, trừ số nguyên
- Cộng hai số nguyên cùng dấu: Cộng như số tự nhiên và giữ nguyên dấu.
- (+5) + (+3) = +8
- (-5) + (-3) = -8
- Cộng hai số nguyên khác dấu: Lấy số có phần giá trị tuyệt đối lớn hơn trừ đi số có phần giá trị tuyệt đối nhỏ hơn, dấu của kết quả là dấu của số có giá trị tuyệt đối lớn hơn.
- (+5) + (-3) = + (5 – 3) = +2
- (-5) + (+3) = – (5 – 3) = -2
- Trừ số nguyên: Muốn trừ số nguyên a cho số nguyên b, ta cộng a với số đối của b: a – b = a + (-b).
- (+5) – (+3) = (+5) + (-3) = +2
- (+5) – (-3) = (+5) + (+3) = +8
- (-5) – (+3) = (-5) + (-3) = -8
- (-5) – (-3) = (-5) + (+3) = -2
Nghe có vẻ hơi phức tạp? Đừng lo, hãy thực hành nhiều và bạn sẽ quen ngay thôi! Giống như việc đi xe đạp vậy đó.
Nhân, chia số nguyên
Quy tắc dấu ở đây đơn giản hơn nhiều:
- Nhân/chia hai số nguyên cùng dấu: Kết quả luôn là số dương (+).
- (+) x (+) = (+) ; (-) x (-) = (+)
- (+) : (+) = (+) ; (-) : (-) = (+)
- Ví dụ: (+6) x (+2) = +12 ; (-6) x (-2) = +12 ; (+6) : (+2) = +3 ; (-6) : (-2) = +3
- Nhân/chia hai số nguyên khác dấu: Kết quả luôn là số âm (-).
- (+) x (-) = (-) ; (-) x (+) = (-)
- (+) : (-) = (-) ; (-) : (+) = (-)
- Ví dụ: (+6) x (-2) = -12 ; (-6) x (+2) = -12 ; (+6) : (-2) = -3 ; (-6) : (+2) = -3
Lưu ý: Phép chia chỉ thực hiện được khi số bị chia chia hết cho số chia (không có dư).
Thứ tự thực hiện phép tính
Giống như với số tự nhiên, khi có nhiều phép tính, chúng ta tuân theo quy tắc: Trong ngoặc trước -> Lũy thừa -> Nhân và Chia (từ trái sang phải) -> Cộng và Trừ (từ trái sang phải).
Giá trị tuyệt đối – Khoảng cách không bao giờ âm
Bạn có để ý thấy khái niệm “giá trị tuyệt đối” khi nói về cộng trừ số nguyên không? Giá trị tuyệt đối của một số nguyên a, ký hiệu là |a|, chính là khoảng cách từ điểm biểu diễn số a đến điểm 0 trên trục số. Vì là khoảng cách nên nó không bao giờ âm.
- |5| = 5 (khoảng cách từ 5 đến 0 là 5 đơn vị)
- |-5| = 5 (khoảng cách từ -5 đến 0 cũng là 5 đơn vị)
- |0| = 0
 Minh họa giá trị tuyệt đối trên trục số
Minh họa giá trị tuyệt đối trên trục số
Caption: Giá trị tuyệt đối |a| là khoảng cách từ điểm a đến gốc 0 trên trục số, luôn là một giá trị không âm.
So Sánh Số Nguyên: Ai Lớn Hơn Ai?
Làm thế nào để biết -10 lớn hơn hay nhỏ hơn -5? Trục số chính là trợ thủ đắc lực!
- Trên trục số, số nằm bên phải luôn lớn hơn số nằm bên trái.
- Mọi số nguyên dương đều lớn hơn 0.
- Mọi số nguyên âm đều nhỏ hơn 0.
- Mọi số nguyên dương đều lớn hơn mọi số nguyên âm.
- Để so sánh hai số nguyên âm, số nào có giá trị tuyệt đối nhỏ hơn thì số đó lớn hơn (nghe ngược đời nhưng đúng đấy!). Ví dụ: |-5| = 5, |-10| = 10. Vì 5 < 10 nên -5 > -10. (Nhìn trên trục số, -5 nằm bên phải -10).
Câu hỏi thường gặp: Số nguyên âm nào lớn nhất?
Trả lời: Đó là số -1. Nó là số nguyên âm gần số 0 nhất về phía bên trái.
Tại Sao Số Nguyên Lại Quan Trọng? Ứng Dụng Thực Tế Không Ngờ
Bạn có thể nghĩ: “Biết về số nguyên thì có ích gì ngoài việc làm toán?”. Câu trả lời là: Rất nhiều! Số nguyên len lỏi vào mọi ngóc ngách của cuộc sống và khoa học.
Trong đời sống hàng ngày
- Nhiệt độ: Nhiệt độ dưới 0°C được biểu thị bằng số nguyên âm.
- Tài chính: Ghi nợ, báo lỗ, số dư âm trong tài khoản… đều dùng số nguyên âm. Số tiền bạn có là số nguyên dương.
- Độ cao: Độ cao so với mực nước biển (dương) và độ sâu dưới mực nước biển (âm).
- Thang máy: Tầng trệt (0), các tầng trên (1, 2, 3…), tầng hầm (B1, B2… tương ứng -1, -2…).
- Thời gian: Trước Công Nguyên (ví dụ: năm 100 TCN có thể coi là -100) và Sau Công Nguyên.
- Game: Điểm số có thể bị trừ (âm) khi phạm lỗi.
Trong khoa học và kỹ thuật
- Vật lý: Điện tích âm, điện tích dương.
- Hóa học: Số oxi hóa của các nguyên tố.
- Khoa học máy tính: Cách máy tính lưu trữ và xử lý số có dấu. Các phép toán bitwise.
- Thống kê: Biểu thị sự thay đổi tăng (dương) hoặc giảm (âm).
Thấy chưa? Số nguyên không chỉ là lý thuyết suông, chúng giúp chúng ta mô tả thế giới xung quanh một cách chính xác và đầy đủ hơn rất nhiều! Việc hiểu và vận dụng thành thạo số nguyên là nền tảng cực kỳ quan trọng cho việc học các kiến thức toán học cao hơn và ứng dụng vào thực tế.
Cách “Làm Chủ” Số Nguyên: Bí Kíp Cho Bạn
Để thực sự hiểu và sử dụng số nguyên một cách tự tin, đây là vài gợi ý:
- Nắm vững khái niệm: Hiểu rõ định nghĩa, các thành phần (dương, âm, 0) và ký hiệu Z.
- Sử dụng trục số thường xuyên: Đây là công cụ trực quan hóa tuyệt vời, giúp bạn hiểu về vị trí, so sánh và cả các phép toán đơn giản.
- Luyện tập các phép toán: Thực hành cộng, trừ, nhân, chia thường xuyên với các loại số nguyên khác nhau. Bắt đầu từ ví dụ đơn giản rồi tăng dần độ khó. Ghi nhớ quy tắc dấu!
- Tìm ví dụ thực tế: Liên hệ kiến thức số nguyên với các tình huống bạn gặp hàng ngày (nhiệt độ, tiền bạc, độ cao…). Điều này giúp kiến thức trở nên sống động và dễ nhớ hơn.
- Đừng ngại hỏi: Nếu có bất kỳ thắc mắc nào, đừng ngần ngại hỏi thầy cô, bạn bè hoặc tìm kiếm trên các nguồn đáng tin cậy như Tailieusieucap.com 😉.
Ý Nghĩa Của Việc Hiểu Rõ Số Nguyên
Việc nắm vững kiến thức về số nguyên mang lại cho bạn nhiều lợi ích:
- Kiến thức nền tảng: Là cơ sở để học tiếp các phần toán phức tạp hơn như phân số, số hữu tỉ, số thực, đại số…
- Tư duy logic: Giúp rèn luyện khả năng tư duy trừu tượng, suy luận logic và giải quyết vấn đề một cách có hệ thống.
- Ứng dụng thực tế: Giúp bạn hiểu và diễn giải các thông tin liên quan đến số âm, số dương trong cuộc sống hàng ngày và trong nhiều lĩnh vực khoa học, kỹ thuật.
- Tự tin hơn: Khi làm chủ được một khái niệm toán học quan trọng, bạn sẽ cảm thấy tự tin hơn vào khả năng học tập của mình.
Kết Luận: Số Nguyên – Không Chỉ Là Những Con Số
Vậy là chúng ta đã cùng nhau dạo một vòng quanh thế giới của số nguyên. Từ định nghĩa cơ bản, các thành viên trong gia đình Z, cách biểu diễn trên trục số, các phép toán, cho đến những ứng dụng thực tế không ngờ. Hy vọng rằng, qua bài viết này của Tailieusieucap.com, số nguyên không còn là một khái niệm xa lạ hay khô khan nữa, mà đã trở thành một người bạn quen thuộc, hữu ích trong hành trình học tập và khám phá thế giới của bạn.
Hãy nhớ rằng, việc hiểu rõ những điều cơ bản như số nguyên chính là chìa khóa để mở ra những cánh cửa kiến thức rộng lớn hơn. Đừng ngần ngại luyện tập và ứng dụng chúng nhé!
Bạn thấy bài viết này hữu ích chứ? Bạn có câu hỏi nào khác về số nguyên không? Hãy để lại bình luận bên dưới, chúng tôi rất mong nhận được phản hồi từ bạn! Và đừng quên chia sẻ bài viết này cho bạn bè nếu bạn thấy nó có giá trị nhé!
Khám phá thêm nhiều tài liệu và kiến thức thú vị khác tại Tailieusieucap.com!