Hình Lăng Trụ: Khám Phá Toàn Diện Từ A-Z Cùng Tailieusieucap.com

Chào các bạn, những người bạn ham học hỏi của Tài Liệu Siêu Cấp! Đã bao giờ bạn nhìn ngắm một tòa nhà cao tầng, một hộp bánh Toblerone độc đáo, hay thậm chí chỉ là một hộp đựng bút đơn giản và tự hỏi: “Hình dạng này gọi là gì trong toán học nhỉ?”. Rất có thể, bạn đang nhìn thấy một Hình Lăng Trụ đấy!

Hình học không gian đôi khi có vẻ hơi “khó nhằn”, nhưng đừng lo, Tailieusieucap.com ở đây để giúp bạn biến những khái niệm trừu tượng thành những điều dễ hiểu và gần gũi nhất. Trong bài viết này, chúng ta sẽ cùng nhau khám phá mọi ngóc ngách về Hình Lăng Trụ, từ định nghĩa cơ bản, các loại phổ biến, công thức tính toán quan trọng cho đến những ứng dụng thú vị trong đời sống. Sẵn sàng chưa nào? Let’s go!

“Hình lăng trụ” – Người bạn quen thuộc trong thế giới hình học

Vậy chính xác thì hình lăng trụ là gì? Nghe tên có vẻ “học thuật” nhưng thực ra khái niệm này lại khá đơn giản.

Định nghĩa hình lăng trụ: Không hề phức tạp như bạn nghĩ!

Hãy tưởng tượng bạn có hai chiếc bánh quy giống hệt nhau (cùng hình dạng, cùng kích thước) và bạn đặt chúng song song với nhau. Sau đó, bạn dùng những que kem thẳng nối các đỉnh tương ứng của hai chiếc bánh quy lại. Voilà! Hình tạo thành chính là một mô hình đơn giản của hình lăng trụ.

Một cách “chuẩn sách giáo khoa” hơn, hình lăng trụ là một khối đa diện được giới hạn bởi:

Hai đáy: Là hai đa giác bằng nhau và nằm trên hai mặt phẳng song song.
Các mặt bên: Là các hình bình hành nối các cạnh tương ứng của hai đáy.
Các cạnh bên: Là các đoạn thẳng nối các đỉnh tương ứng của hai đáy. Các cạnh bên này luôn song song và bằng nhau.

Dễ hình dung hơn rồi đúng không nào?

Các yếu tố cấu thành nên một hình lăng trụ

Để hiểu rõ hơn về “anh bạn” này, chúng ta cần nắm vững các bộ phận cấu tạo nên nó:

Đáy (Base): Hai đa giác bằng nhau và song song (ví dụ: tam giác, hình vuông, ngũ giác…). Tên của hình lăng trụ thường được gọi theo hình dạng của đáy (ví dụ: hình lăng trụ tam giác, hình lăng trụ tứ giác).
Mặt bên (Lateral Faces): Luôn là các hình bình hành. Số mặt bên bằng số cạnh của đa giác đáy.
Cạnh bên (Lateral Edges): Các đoạn thẳng nối đỉnh tương ứng của hai đáy. Chúng song song và bằng nhau.
Chiều cao (Height – h): Khoảng cách vuông góc giữa hai mặt phẳng đáy. Đây là yếu tố cực kỳ quan trọng khi tính toán thể tích đó nha!

Caption: Sơ đồ cấu tạo cơ bản của một hình lăng trụ giúp bạn dễ dàng nhận biết các thành phần quan trọng.

Phân loại hình lăng trụ: Muôn hình vạn trạng!

Thế giới hình lăng trụ cũng rất đa dạng đấy nhé. Chúng ta có thể phân loại chúng dựa trên một số đặc điểm chính:

Hình lăng trụ đứng và hình lăng trụ xiên: Khác biệt ở đâu?

Đây là cách phân loại dựa vào mối quan hệ giữa cạnh bên và mặt đáy:

Hình lăng trụ đứng (Right Prism): Khi các cạnh bên vuông góc với mặt phẳng đáy. Trong trường hợp này, các mặt bên sẽ là hình chữ nhật, và chiều cao của lăng trụ chính bằng độ dài cạnh bên. Đây là loại lăng trụ chúng ta thường gặp nhất. Bạn có nghĩ ra ví dụ nào không? Đúng rồi, một hộp diêm, một viên gạch xây nhà chính là ví dụ điển hình đó!
Hình lăng trụ xiên (Oblique Prism): Khi các cạnh bên không vuông góc với mặt phẳng đáy. Lúc này, các mặt bên vẫn là hình bình hành (nhưng không phải hình chữ nhật), và chiều cao sẽ là đường vuông góc hạ từ một đỉnh của đáy này xuống mặt phẳng đáy kia (khác với độ dài cạnh bên). Hãy tưởng tượng bạn đẩy nhẹ một chồng sách cho nó hơi nghiêng đi – đó là hình ảnh của lăng trụ xiên.

Bạn có thắc mắc: Làm sao để phân biệt hình lăng trụ đứng và xiên khi nhìn vào hình vẽ không gian? Hãy chú ý đến góc tạo bởi cạnh bên và cạnh đáy nhé!

So sánh hình lăng trụ đứng và xiên
Caption: Sự khác biệt rõ ràng giữa hình lăng trụ đứng (trái) và hình lăng trụ xiên (phải) nằm ở góc của cạnh bên so với đáy.

Gọi tên theo hình dạng đáy: Lăng trụ tam giác, tứ giác, và hơn thế nữa!

Cách phân loại này cực kỳ trực quan:

Hình lăng trụ tam giác: Đáy là hình tam giác (ví dụ: lăng trụ đứng tam giác có đáy là tam giác đều, tam giác vuông…).
Hình lăng trụ tứ giác: Đáy là hình tứ giác (ví dụ: hình hộp chữ nhật, hình lập phương là các trường hợp đặc biệt của lăng trụ đứng tứ giác).
Hình lăng trụ ngũ giác, lục giác…: Đáy là hình ngũ giác, lục giác…

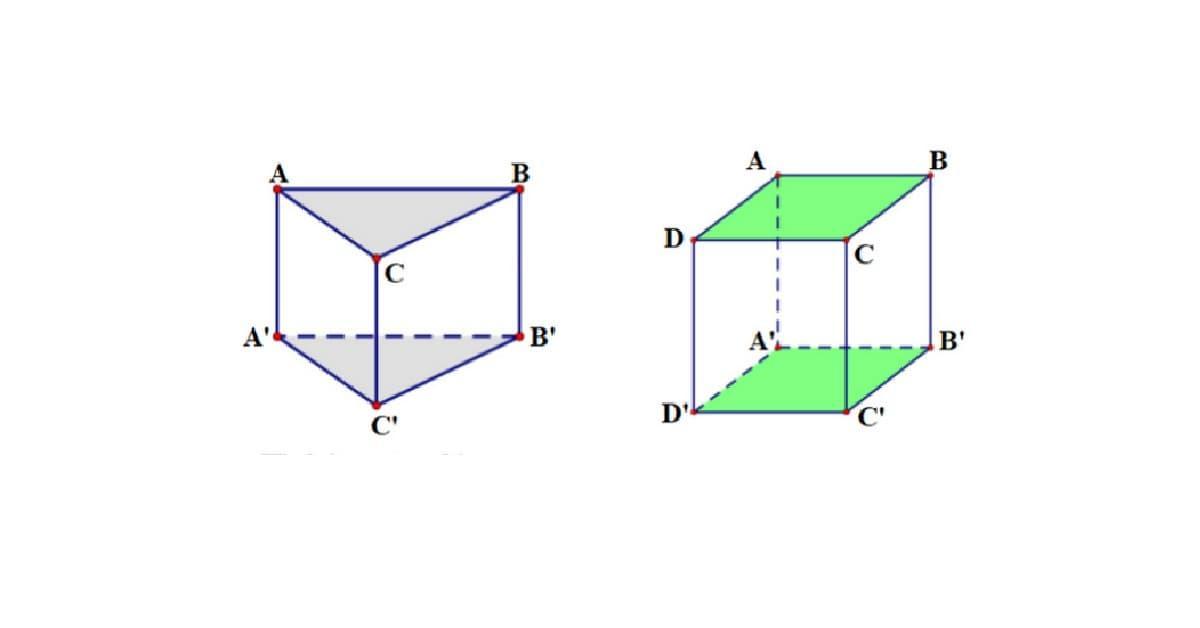Ví dụ về hình lăng trụ tam giác
Caption: Hình lăng trụ tam giác đứng – một dạng phổ biến trong các bài toán hình học.

Caption: Hình hộp chữ nhật quen thuộc thực chất là một hình lăng trụ tứ giác đứng.

Công thức “vàng” giúp bạn chinh phục hình lăng trụ

Đến phần quan trọng mà nhiều bạn mong chờ rồi đây: các công thức tính toán liên quan đến hình lăng trụ. Nắm vững những công thức này sẽ giúp bạn giải quyết ngon lành các bài tập đó!

Làm thế nào để tính diện tích xung quanh hình lăng trụ? (Sxq)

Diện tích xung quanh (Sxq) là tổng diện tích của tất cả các mặt bên.

Đối với hình lăng trụ đứng:
Sxq = Chu vi đáy * Chiều cao (h)
Trong đó chiều cao (h) chính là độ dài cạnh bên.
Đối với hình lăng trụ xiên:
Sxq = Chu vi thiết diện thẳng * Độ dài cạnh bên (l)
(Thiết diện thẳng là mặt cắt tạo bởi mặt phẳng vuông góc với các cạnh bên. Công thức này ít phổ biến hơn trong chương trình phổ thông).

Vậy nếu đề bài cho lăng trụ đứng tam giác đều cạnh a, chiều cao h thì Sxq tính sao nhỉ? Chu vi đáy là 3a, vậy Sxq = 3a * h. Đơn giản đúng không?

Tính diện tích toàn phần (Stp) có khó không?

Diện tích toàn phần (Stp) là tổng diện tích xung quanh và diện tích của cả hai mặt đáy.

Stp = Sxq + 2 * Diện tích đáy (Sđáy)

Chỉ cần bạn tính được Sxq và diện tích đáy là xong!

Thể tích hình lăng trụ (V) – Công thức bạn không thể bỏ qua!

Đây là công thức quan trọng nhất và áp dụng cho mọi loại hình lăng trụ (cả đứng và xiên):

V = Diện tích đáy (Sđáy) * Chiều cao (h)

Lưu ý quan trọng:

Chiều cao (h) luôn là khoảng cách vuông góc giữa hai mặt phẳng đáy.
Với lăng trụ đứng, chiều cao (h) bằng độ dài cạnh bên.
Với lăng trụ xiên, chiều cao (h) không phải là độ dài cạnh bên (trừ khi đề bài cho đặc biệt). Bạn cần xác định hoặc tính toán đường cao này.

Một câu hỏi thường gặp: Thể tích hình hộp chữ nhật có phải tuân theo công thức này không? Chính xác! Hình hộp chữ nhật có đáy là hình chữ nhật diện tích a*b, chiều cao là c. Vậy V = (a*b)*c, đúng công thức thể tích chúng ta đã biết!

Hình lăng trụ trong đời sống: Không chỉ là lý thuyết suông!

Bạn có nghĩ rằng hình lăng trụ chỉ tồn tại trong sách vở toán học? Không hề đâu! Hãy nhìn xung quanh mà xem:

Những ví dụ thực tế thú vị

Kiến trúc: Rất nhiều tòa nhà, cột nhà có dạng hình lăng trụ đứng (thường là lăng trụ tứ giác).
Đóng gói: Vô số hộp đựng sản phẩm (hộp sữa, hộp bánh, thùng carton…) là hình lăng trụ. Thanh socola Toblerone nổi tiếng có dạng lăng trụ tam giác.
Thiên nhiên: Một số tinh thể khoáng sản có cấu trúc dạng lăng trụ.
Quang học: Lăng kính (thường là lăng trụ tam giác) dùng để tán sắc ánh sáng là một ứng dụng vật lý quan trọng.

Ứng dụng của hình lăng trụ trong thực tế
Caption: Hình lăng trụ xuất hiện đa dạng trong cuộc sống, từ kiến trúc, đóng gói đến các hiện tượng vật lý.

Tại sao hiểu về hình lăng trụ lại quan trọng?

Việc nắm vững kiến thức về hình lăng trụ mang lại nhiều lợi ích:

Nền tảng Toán học: Là kiến thức cơ bản và quan trọng trong chương trình hình học không gian, tiền đề để học các khối đa diện phức tạp hơn.
Tư duy không gian: Giúp rèn luyện khả năng tưởng tượng, hình dung các vật thể trong không gian ba chiều.
Giải quyết vấn đề: Áp dụng các công thức để giải các bài toán thực tế liên quan đến tính toán diện tích, thể tích (ví dụ: tính lượng vật liệu cần thiết, dung tích chứa…).
Liên ngành: Kiến thức này có ứng dụng trong nhiều lĩnh vực khác như vật lý (quang học), kỹ thuật, kiến trúc, thiết kế đồ họa 3D…

Giải đáp thắc mắc thường gặp về hình lăng trụ (FAQs)

Trong quá trình tìm hiểu, chắc hẳn bạn sẽ có một vài câu hỏi. Tailieusieucap.com đã tổng hợp một số thắc mắc phổ biến:

Câu hỏi 1: Mọi hình lăng trụ đều có mặt bên là hình bình hành đúng không?
- Trả lời: Đúng! Đây là một phần của định nghĩa hình lăng trụ. Đặc biệt, với lăng trụ đứng, các mặt bên là hình chữ nhật.
Câu hỏi 2: Chiều cao và cạnh bên của hình lăng trụ có luôn bằng nhau không?
- Trả lời: Chỉ bằng nhau trong trường hợp hình lăng trụ đứng. Đối với lăng trụ xiên, cạnh bên thường dài hơn chiều cao.
Câu hỏi 3: Làm sao để tính thể tích hình lăng trụ xiên khi chỉ biết cạnh bên và góc nghiêng?
- Trả lời: Bạn cần sử dụng lượng giác để tìm chiều cao (h). Nếu biết góc α giữa cạnh bên (l) và mặt đáy, thì h = l * sin(α). Sau đó áp dụng công thức V = Sđáy * h.

Mẹo nhỏ giúp bạn học tốt phần hình lăng trụ

Để “kết thân” dễ dàng hơn với hình lăng trụ, hãy thử áp dụng những mẹo sau:

Vẽ hình chuẩn: Một hình vẽ rõ ràng, chính xác (đặc biệt là phân biệt nét liền, nét đứt) sẽ giúp bạn hình dung bài toán tốt hơn rất nhiều. Đừng ngại vẽ lại hình nếu hình ban đầu chưa ổn.
Nắm chắc công thức: Hãy hiểu rõ ý nghĩa từng đại lượng trong công thức (Sđáy, h, chu vi đáy…) chứ không chỉ học vẹt.
Làm bài tập từ dễ đến khó: Bắt đầu với các bài tập cơ bản về lăng trụ đứng, sau đó mới chuyển sang lăng trụ xiên và các bài toán phức tạp hơn.
Liên hệ thực tế: Thử tìm các vật thể có dạng lăng trụ xung quanh bạn và ước lượng thử kích thước, thể tích của chúng. Điều này giúp kiến thức bớt khô khan hơn.
Sử dụng tài liệu tham khảo: Đừng ngần ngại tìm đọc thêm các chuyên đề, bài giảng về hình lăng trụ trên Tailieusieucap.com hay các nguồn uy tín khác.

[internal_links]

(Có thể chèn link đến các bài viết khác trên Tailieusieucap.com như: “Công thức tính thể tích khối đa diện”, “Bài tập hình học không gian lớp 11/12 có lời giải”, “Phân biệt các loại khối đa diện”, v.v…)

Kết luận

Vậy là chúng ta đã cùng nhau đi qua một hành trình khám phá khá chi tiết về hình lăng trụ. Từ định nghĩa, phân loại, các công thức tính toán quan trọng cho đến ứng dụng thực tế, hy vọng rằng giờ đây, khái niệm hình lăng trụ đã trở nên gần gũi và dễ hiểu hơn với bạn.

Hãy nhớ rằng, việc nắm vững kiến thức về hình lăng trụ không chỉ giúp bạn đạt điểm cao trong môn Toán mà còn rèn luyện tư duy logic, khả năng hình dung không gian – những kỹ năng vô cùng hữu ích trong cuộc sống. Đừng coi hình học là một “gánh nặng”, hãy xem nó như một công cụ tuyệt vời để khám phá thế giới xung quanh bạn!

Tailieusieucap.com luôn đồng hành cùng bạn trên con đường chinh phục tri thức. Nếu bạn có bất kỳ câu hỏi nào khác về hình lăng trụ hay các chủ đề khác, đừng ngần ngại để lại bình luận bên dưới nhé! Hãy chia sẻ bài viết này nếu bạn thấy nó hữu ích và tiếp tục khám phá thêm nhiều Tài Liệu Siêu Cấp khác trên website của chúng mình! Chúc các bạn học tốt!