Chào các bạn độc giả thân mến của Tài Liệu Siêu Cấp! Đã bao giờ bạn ném một quả bóng lên trời và tò mò về quỹ đạo cong cong mà nó vẽ ra chưa? Hay bạn từng ngắm nhìn một cây cầu dây văng đồ sộ và tự hỏi hình dáng đó có tên gọi gì trong toán học? Câu trả lời nằm ở một khái niệm vô cùng quen thuộc nhưng cũng đầy thú vị: Hình Parabol.
Trong bài viết này, chúng ta sẽ cùng nhau “mổ xẻ” mọi thứ về Hình Parabol, từ định nghĩa cơ bản nhất đến những ứng dụng không ngờ trong cuộc sống. Dù bạn đang ôn thi, tìm hiểu kiến thức, hay đơn giản là tò mò, hãy cùng Tailieusieucap.com khám phá thế giới hấp dẫn của đường cong này nhé! Biết đâu, sau bài viết này, bạn sẽ nhìn thế giới xung quanh với một con mắt “toán học” hơn thì sao? 😉
Hình Parabol Là Gì? Khám Phá Đường Cong Quen Thuộc Mà Đầy Bí Ẩn
Nhiều người nghe đến “parabol” là nghĩ ngay đến đồ thị hàm số bậc hai trong sách giáo khoa Toán. Điều đó đúng, nhưng chưa đủ! Vậy bản chất thực sự của hình parabol là gì?
Định nghĩa “chuẩn sách giáo khoa”
Một cách chính xác, hình parabol là tập hợp tất cả các điểm trong một mặt phẳng cách đều một điểm cố định cho trước (gọi là tiêu điểm – Focus, ký hiệu là F) và một đường thẳng cố định cho trước (gọi là đường chuẩn – Directrix, ký hiệu là Δ). Khoảng cách từ một điểm bất kỳ trên parabol đến tiêu điểm bằng khoảng cách từ điểm đó đến đường chuẩn.
Nghe có vẻ hơi “hack não” phải không? Đừng lo lắng, hãy hình dung thế này:
 Minh họa định nghĩa hình parabol
Minh họa định nghĩa hình parabol
Caption: Hình ảnh minh họa trực quan định nghĩa của một hình parabol: mọi điểm M trên đường cong đều cách đều tiêu điểm F và đường chuẩn Δ.
Hình dung parabol qua các ví dụ đời thường
Bạn có thấy quen thuộc không? Hình parabol xuất hiện ở khắp mọi nơi:
- Đường nước phun từ vòi: Lần tới khi thấy vòi phun nước công cộng, hãy để ý quỹ đạo của dòng nước nhé!
- Quỹ đạo của vật bị ném: Khi bạn ném một quả bóng rổ, quả cầu tuyết, hay bất cứ vật gì (bỏ qua sức cản không khí), nó sẽ bay theo một đường parabol.
- Chóa đèn pha ô tô, xe máy: Thiết kế dạng parabol giúp hội tụ ánh sáng từ bóng đèn thành một chùm sáng song song, chiếu xa hơn.
- Ăng-ten vệ tinh (chảo parabol): Hình dáng parabol giúp thu sóng tín hiệu từ vệ tinh và hội tụ chúng vào bộ thu đặt tại tiêu điểm.
Vậy đấy, hình parabol không hề xa vời mà hiện diện ngay trong cuộc sống hàng ngày của chúng ta!
Giải Mã Phương Trình Parabol – “Công Thức Vàng” Của Đường Cong
Để làm việc với parabol trong toán học, chúng ta cần biểu diễn nó dưới dạng phương trình. Phương trình parabol giúp xác định chính xác vị trí và hình dạng của đường cong này.
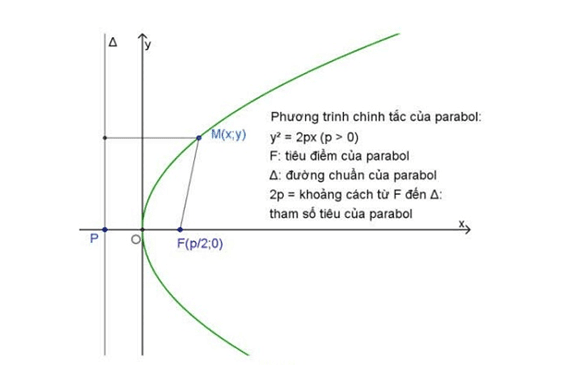
Phương trình chính tắc của parabol
Tùy thuộc vào vị trí của tiêu điểm và đường chuẩn so với hệ trục tọa độ Oxy, parabol sẽ có các dạng phương trình chính tắc khác nhau. Dạng phổ biến nhất mà chúng ta thường gặp trong chương trình học là:
-
Parabol có trục đối xứng là Ox, đỉnh O(0,0):
- Phương trình: y² = 4px (với p ≠ 0)
- Tiêu điểm F(p, 0)
- Đường chuẩn Δ: x = -p
- Nếu p > 0, parabol quay bề lõm sang phải.
- Nếu p < 0, parabol quay bề lõm sang trái.
-
Parabol có trục đối xứng là Oy, đỉnh O(0,0):
- Phương trình: x² = 4py (với p ≠ 0)
- Tiêu điểm F(0, p)
- Đường chuẩn Δ: y = -p
- Nếu p > 0, parabol quay bề lõm lên trên (đây chính là đồ thị hàm số y = ax² khi a > 0 và p = 1/(4a)).
- Nếu p < 0, parabol quay bề lõm xuống dưới (đồ thị hàm số y = ax² khi a < 0 và p = 1/(4a)).
Tham số tiêu p đóng vai trò cực kỳ quan trọng, nó quyết định khoảng cách từ đỉnh đến tiêu điểm và từ đỉnh đến đường chuẩn (|p|), đồng thời ảnh hưởng đến độ “mở” của parabol.
Các yếu tố quan trọng: Đỉnh, Tiêu điểm, Đường chuẩn, Trục đối xứng
Để hiểu rõ một hình parabol, bạn cần nắm vững các yếu tố cấu thành nên nó:
- Đỉnh (Vertex): Là điểm nằm giữa tiêu điểm và đường chuẩn, nơi parabol “uốn cong” nhất. Trong phương trình chính tắc cơ bản, đỉnh là gốc tọa độ O(0,0). Với đồ thị hàm số y = ax² + bx + c, đỉnh có tọa độ I(-b/2a, -Δ/4a).
- Tiêu điểm (Focus – F): Điểm cố định mà mọi điểm trên parabol cách đều nó và đường chuẩn. Đây là “trái tim” quyết định tính chất hội tụ/phân kỳ của parabol.
- Đường chuẩn (Directrix – Δ): Đường thẳng cố định mà mọi điểm trên parabol cách đều nó và tiêu điểm.
- Trục đối xứng (Axis of Symmetry): Đường thẳng đi qua đỉnh và tiêu điểm, chia parabol thành hai nhánh đối xứng hoàn hảo.
Caption: Sơ đồ minh họa các thành phần chính của một parabol dạng y² = 4px: Đỉnh, Tiêu điểm, Đường chuẩn và Trục đối xứng.
Cách xác định các yếu tố từ phương trình
Bạn đang băn khoăn làm sao để tìm tiêu điểm và đường chuẩn của parabol khi chỉ có phương trình? Rất đơn giản!
- Bước 1: Đưa phương trình parabol về dạng chính tắc (y² = 4px hoặc x² = 4py). Nếu là phương trình tổng quát của hàm bậc hai y = ax² + bx + c, bạn cần tìm đỉnh I(-b/2a, -Δ/4a) và xác định tham số tiêu p = 1/(4a).
- Bước 2: Xác định giá trị của ‘p’. Dấu của ‘p’ cho biết hướng quay của parabol.
- Bước 3: Dựa vào dạng phương trình và giá trị ‘p’, xác định tọa độ tiêu điểm và phương trình đường chuẩn theo công thức tương ứng đã nêu ở trên.
Ví dụ: Cho parabol (P): y² = 8x.
Ta thấy phương trình có dạng y² = 4px, suy ra 4p = 8 => p = 2.
Vì p > 0 và trục đối xứng là Ox, parabol quay sang phải.
Vậy:
- Đỉnh: O(0,0)
- Tiêu điểm: F(p, 0) = F(2, 0)
- Đường chuẩn: Δ: x = -p => x = -2
Làm Thế Nào Để Vẽ Một Hình Parabol Chính Xác?
Vẽ parabol không hề khó nếu bạn nắm được các bước cơ bản. Dù là vẽ đồ thị hàm số bậc hai hay vẽ parabol từ phương trình chính tắc, quy trình thường bao gồm:
Các bước cơ bản để phác thảo đồ thị
- Xác định đỉnh: Tìm tọa độ đỉnh của parabol. Đây là điểm khởi đầu quan trọng nhất.
- Xác định trục đối xứng: Vẽ đường thẳng đi qua đỉnh và song song với trục tương ứng (Ox hoặc Oy tùy dạng phương trình).
- Xác định hướng quay (bề lõm): Dựa vào dấu của ‘p’ (hoặc dấu của ‘a’ trong y = ax² + bx + c).
- Tìm tiêu điểm và đường chuẩn (nếu cần): Giúp xác định độ “mở” chính xác hơn, đặc biệt trong các bài toán quang học hoặc hình học giải tích.
- Lấy thêm một vài điểm đối xứng: Chọn một vài giá trị x (hoặc y) và tính giá trị y (hoặc x) tương ứng. Sau đó lấy điểm đối xứng qua trục đối xứng. Càng nhiều điểm, parabol càng chính xác.
- Nối các điểm: Vẽ một đường cong mượt mà đi qua đỉnh và các điểm đã xác định, đảm bảo đối xứng qua trục.
Mẹo nhỏ giúp bạn vẽ đẹp và nhanh hơn
- Hãy nhớ rằng parabol càng “mở rộng” khi giá trị tuyệt đối của ‘p’ càng lớn (hoặc |a| càng nhỏ).
- Sử dụng tính đối xứng để giảm một nửa công việc lấy điểm.
- Nếu vẽ đồ thị hàm số y = ax² + bx + c, ngoài đỉnh, hãy tìm giao điểm với trục tung (tại x=0, y=c) và trục hoành (giải ax² + bx + c = 0) nếu có.
Ứng Dụng Kỳ Diệu Của Hình Parabol Trong Cuộc Sống Và Khoa Học
Bạn có tin rằng đường cong tưởng chừng đơn giản này lại ẩn chứa những ứng dụng vô cùng quan trọng không? Tính chất của parabol chính là chìa khóa!
Đặc tính quan trọng nhất của parabol là tính chất quang học (phản xạ): Mọi tia sáng song song với trục đối xứng khi chiếu vào mặt trong của parabol sẽ phản xạ và hội tụ tại tiêu điểm. Ngược lại, nếu đặt nguồn sáng tại tiêu điểm, các tia sáng sau khi phản xạ qua parabol sẽ trở thành một chùm tia song song với trục đối xứng.
Từ chiếc đèn pha ô tô đến kính thiên văn khổng lồ
- Đèn pha, đèn pin: Chóa đèn có dạng mặt paraboloid (hình tạo bởi parabol quay quanh trục đối xứng). Bóng đèn đặt tại tiêu điểm, giúp tạo ra chùm sáng song song chiếu xa.
- Bếp mặt trời: Sử dụng gương parabol lớn để hội tụ ánh nắng mặt trời vào tiêu điểm, tạo ra nhiệt độ cao để đun nấu.
- Kính thiên văn phản xạ: Gương chính có dạng parabol giúp hội tụ ánh sáng từ các thiên thể xa xôi vào tiêu điểm, nơi đặt bộ thu hoặc gương phụ.
- Antenna parabol (chảo vệ tinh): Thu sóng điện từ song song từ vệ tinh và hội tụ chúng vào bộ thu đặt tại tiêu điểm.
 Minh họa các ứng dụng của parabol
Minh họa các ứng dụng của parabol
Caption: Hình parabol không chỉ là lý thuyết suông, nó hiện hữu trong công nghệ từ đèn pha, chảo vệ tinh đến các công trình kiến trúc vĩ đại.
Trong kiến trúc và kỹ thuật
- Cầu treo: Dây cáp chính của nhiều cây cầu treo nổi tiếng (như cầu Cổng Vàng) có hình dạng gần giống parabol (mặc dù chính xác hơn là đường dây xích – catenary, nhưng parabol là một xấp xỉ tốt và dễ tính toán hơn). Hình dáng này giúp phân bổ lực căng một cách hiệu quả.
- Mái vòm, kết cấu parabol: Một số công trình kiến trúc sử dụng mái vòm hoặc kết cấu dạng parabol để tăng khả năng chịu lực và tạo không gian độc đáo.
Đường bay của vật thể
Như đã đề cập, trong điều kiện lý tưởng (bỏ qua sức cản không khí), quỹ đạo của một vật được ném lên xiên góc với phương ngang là một hình parabol. Hiểu biết này rất quan trọng trong vật lý, đặc biệt là đạn đạo học.
Những Câu Hỏi Thường Gặp Về Hình Parabol (FAQ)
Trong quá trình tìm hiểu, chắc hẳn bạn sẽ có vài thắc mắc. Tailieusieucap.com đã tổng hợp một số câu hỏi phổ biến:
- Hỏi: Parabol có phải luôn là đồ thị của hàm số bậc hai y = ax² + bx + c không?
- Đáp: Không hoàn toàn. Đồ thị hàm số y = ax² + bx + c (với a ≠ 0) luôn là một parabol có trục đối xứng song song hoặc trùng với trục Oy. Tuy nhiên, các parabol có trục đối xứng song song hoặc trùng với trục Ox (dạng x = ay² + by + c) không phải là đồ thị của một hàm số theo biến x (vì một giá trị x có thể tương ứng với hai giá trị y).
- Hỏi: Tiêu điểm của parabol có ý nghĩa thực tế gì?
- Đáp: Như đã giải thích ở phần ứng dụng, tiêu điểm là nơi hội tụ năng lượng (ánh sáng, sóng điện từ, âm thanh) khi chúng phản xạ từ bề mặt parabol. Đây là chìa khóa cho các ứng dụng như ăng-ten, kính thiên văn, đèn pha.
- Hỏi: Làm sao phân biệt parabol với các đường conic khác như Elip hay Hypebol?
- Đáp: Cả ba đều là đường conic, tạo thành từ giao của mặt nón và mặt phẳng. Điểm khác biệt cơ bản nằm ở “độ lệch tâm” (eccentricity – e). Parabol có e = 1. Elip có 0 ≤ e < 1 (đường tròn là trường hợp đặc biệt e = 0). Hypebol có e > 1. Về hình dạng, elip là đường cong khép kín, hypebol có hai nhánh riêng biệt, còn parabol chỉ có một nhánh và mở ra vô hạn.
Ý Nghĩa Của Việc Hiểu Rõ Hình Parabol
Việc dành thời gian tìm hiểu về hình parabol mang lại nhiều lợi ích hơn bạn nghĩ:
Nền tảng kiến thức toán học vững chắc
Parabol là một phần quan trọng trong chương trình Hình học giải tích và Đại số. Nắm vững kiến thức về parabol giúp bạn giải quyết tốt các bài toán liên quan đến khảo sát hàm số, viết phương trình đường conic, và các bài toán tối ưu hóa có liên quan.
Mở rộng tư duy, nhìn thế giới qua lăng kính toán học
Khi hiểu về parabol, bạn sẽ bắt đầu nhận ra sự hiện diện của nó trong thế giới tự nhiên và công nghệ xung quanh. Điều này giúp bạn thấy được vẻ đẹp và tính ứng dụng của toán học, không còn coi nó là môn học khô khan nữa.
Công cụ giải quyết các bài toán thực tế
Kiến thức về parabol có thể áp dụng vào việc giải quyết các vấn đề thực tế trong vật lý (quỹ đạo, quang học), kỹ thuật (thiết kế cầu, ăng-ten), và thậm chí là kinh tế (mô hình hóa chi phí, lợi nhuận).
Kết Luận
Vậy là chúng ta đã cùng nhau đi qua một hành trình khám phá hình parabol, từ định nghĩa, phương trình, cách vẽ cho đến những ứng dụng thực tế đầy bất ngờ. Hy vọng rằng qua bài viết này của Tailieusieucap.com, đường cong parabol không còn là một khái niệm xa lạ hay khó nhằn nữa, mà đã trở thành một người bạn quen thuộc, một công cụ hữu ích trong kho tàng kiến thức của bạn.
Toán học luôn ẩn chứa những điều thú vị và hình parabol chính là một minh chứng sống động. Hãy tiếp tục khám phá, tìm tòi và đừng ngần ngại đặt câu hỏi nhé!
Bạn thấy ứng dụng nào của parabol là thú vị nhất? Bạn có câu hỏi nào khác về chủ đề này không? Hãy để lại bình luận bên dưới, chúng tôi rất mong nhận được phản hồi từ bạn. Đừng quên chia sẻ bài viết này nếu bạn thấy nó hữu ích và khám phá thêm nhiều Tài Liệu Siêu Cấp khác tại Tailieusieucap.com nhé!
[internal_links]
Lưu ý: Nội dung bài viết mang tính chất cung cấp kiến thức toán học và ứng dụng khoa học, hoàn toàn không liên quan hay cổ súy cho các hoạt động mê tín dị đoan, cờ bạc. Thông tin được trình bày dựa trên kiến thức toán học phổ thông và các ứng dụng thực tế được công nhận rộng rãi.