Bạn đã bao giờ cảm thấy “rối não” khi phải giải một hệ phương trình với cả tá ẩn số? Hay tò mò làm thế nào mà máy tính có thể tạo ra những hình ảnh 3D sống động trong game hay phim ảnh? Có một “bí kíp” đằng sau những điều đó, và tên của nó chính là Ma Trận.
Nghe có vẻ hơi “hàn lâm” phải không? Đừng lo lắng! Trong bài viết này, chúng ta sẽ cùng nhau “bóc tách” khái niệm Ma Trận một cách gần gũi, dễ hiểu nhất, như thể đang trò chuyện với một người bạn vậy. Dù bạn là học sinh, sinh viên đang vật lộn với môn Đại số tuyến tính, một lập trình viên muốn tối ưu thuật toán, hay đơn giản là một người tò mò muốn khám phá thế giới, bài viết này chắc chắn sẽ hữu ích. Cùng tìm hiểu ma trận là gì và tại sao nó lại quan trọng đến thế nhé!
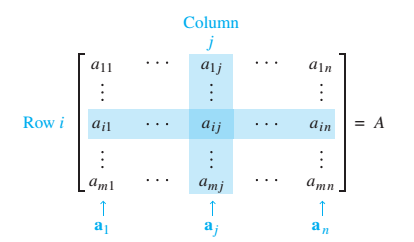Khái niệm cơ bản về Ma Trận
Caption: Đừng để những con số và dấu ngoặc làm bạn sợ hãi! Ma trận thực chất là một cách sắp xếp thông tin cực kỳ logic và hiệu quả.
“Ma Trận” – Không Chỉ Là Những Con Số Trong Khung Vuông!
Vậy rốt cuộc, ma trận là gì?
Định nghĩa “chuẩn sách giáo khoa” nhưng dễ hiểu về Ma trận
Nói một cách đơn giản nhất, ma trận (tiếng Anh: Matrix) là một bảng hình chữ nhật chứa các số, ký hiệu hoặc biểu thức, được sắp xếp thành các hàng (row) và cột (column). Cứ tưởng tượng nó như một cái bảng tính Excel thu nhỏ vậy, nhưng quyền năng hơn nhiều!
Ví dụ:
Một ma trận A có 2 hàng và 3 cột có thể trông như thế này:
[ 1 5 -2 ]
A = [ 3 0 7 ]Ma trận này được gọi là ma trận cấp 2×3 (đọc là 2 nhân 3). Mỗi phần tử trong ma trận được xác định bởi vị trí hàng và cột của nó. Ví dụ, phần tử ở hàng 1, cột 2 là số 5.
Tại sao chúng ta lại cần đến Ma trận? Sức mạnh tiềm ẩn là gì?
“Okay, hiểu rồi, nó là cái bảng số. Nhưng dùng nó để làm gì mới được chứ?” – Có lẽ bạn đang thắc mắc như vậy.
Sức mạnh của ma trận nằm ở chỗ nó cung cấp một cách biểu diễn dữ liệu và thực hiện các phép toán phức tạp một cách cực kỳ gọn gàng và hiệu quả. Thay vì viết hàng loạt phương trình dài dòng, bạn có thể gói gọn chúng vào một vài ma trận. Điều này giúp chúng ta:
- Giải quyết các hệ phương trình tuyến tính lớn: Đây là một trong những ứng dụng đầu tiên và quan trọng nhất.
- Biểu diễn các phép biến đổi hình học: Phóng to, thu nhỏ, xoay, lật ảnh trong đồ họa máy tính? Ma trận làm được hết!
- Lưu trữ và xử lý dữ liệu: Trong khoa học dữ liệu, ma trận dùng để biểu diễn các tập dữ liệu khổng lồ.
- Mô hình hóa các hệ thống phức tạp: Từ mạng lưới kinh tế đến các thuật toán trong trí tuệ nhân tạo (AI).
Nghe hấp dẫn rồi đúng không? Hãy cùng khám phá sâu hơn các loại ma trận phổ biến nhé!
Khám Phá Thế Giới Đa Dạng Của Các Loại Ma Trận
Không phải ma trận nào cũng giống nhau. Tùy thuộc vào hình dạng và tính chất, chúng ta có nhiều “gương mặt” ma trận khác nhau:
Ma trận vuông, ma trận hàng, ma trận cột – Những “gương mặt” quen thuộc
- Ma trận vuông: Là ma trận có số hàng bằng số cột (ví dụ: ma trận 2×2, 3×3). Đây là loại ma trận cực kỳ quan trọng, liên quan đến nhiều khái niệm như định thức, ma trận nghịch đảo. Bạn có thắc mắc ma trận vuông là gì không? Đơn giản là nó “vuông vức” thôi!
- Ma trận hàng: Chỉ có một hàng duy nhất (ví dụ: ma trận 1×4).
- Ma trận cột: Chỉ có một cột duy nhất (ví dụ: ma trận 3×1). Thường được dùng để biểu diễn các vector.
Ma trận đơn vị, ma trận không – “Nhân vật” đặc biệt
- Ma trận không: Tất cả các phần tử đều bằng 0. Nó giống như số 0 trong phép cộng thông thường vậy.
- Ma trận đơn vị (Identity Matrix – I): Là một ma trận vuông đặc biệt, có các phần tử trên đường chéo chính bằng 1, còn lại bằng 0. Nó đóng vai trò như số 1 trong phép nhân ma trận.
[ 1 0 0 ] I = [ 0 1 0 ] [ 0 0 1 ] (Đây là ma trận đơn vị cấp 3)
Ma trận chuyển vị, ma trận nghịch đảo – Các phép biến hình thú vị
- Ma trận chuyển vị (Transpose – AT): Có được bằng cách “lật” ma trận gốc qua đường chéo chính, tức là đổi hàng thành cột và cột thành hàng.
- Ma trận nghịch đảo (Inverse – A-1): Chỉ tồn tại với một số ma trận vuông đặc biệt (có định thức khác 0). Khi nhân ma trận gốc với ma trận nghịch đảo của nó (hoặc ngược lại), kết quả sẽ là ma trận đơn vị (A A-1 = A-1 A = I). Khái niệm ma trận nghịch đảo là gì nghe có vẻ phức tạp, nhưng nó cực kỳ hữu ích để “chia” trong thế giới ma trận đấy!
“Múa” Cùng Các Phép Toán Ma Trận Cơ Bản
Giống như các con số thông thường, chúng ta cũng có thể thực hiện các phép toán trên ma trận.
Các phép toán cơ bản trên ma trận
Caption: Các phép toán ma trận có quy tắc riêng, nhưng một khi đã nắm vững, bạn sẽ thấy chúng rất logic.
Phép cộng, trừ ma trận: Đơn giản như 1+1?
Để cộng hoặc trừ hai ma trận, chúng phải có cùng kích thước (cùng số hàng, cùng số cột). Bạn chỉ cần cộng hoặc trừ các phần tử ở vị trí tương ứng. Khá đơn giản phải không?
Ví dụ cộng ma trận:
[ 1 2 ] + [ 5 6 ] = [ 1+5 2+6 ] = [ 6 8 ]
[ 3 4 ] [ 7 8 ] [ 3+7 4+8 ] [ 10 12 ]Phép nhân ma trận: Có chút “hack não” nhưng cực kỳ quyền năng
Phép nhân ma trận phức tạp hơn một chút. Để nhân ma trận A với ma trận B (A * B), số cột của A phải bằng số hàng của B. Kết quả sẽ là một ma trận C, trong đó mỗi phần tử Cij (hàng i, cột j) được tính bằng cách lấy “tích vô hướng” của hàng i của A và cột j của B.
Lưu ý quan trọng: Phép nhân ma trận không có tính giao hoán, tức là A B thường khác B A. Đây là điểm khác biệt lớn so với phép nhân số thông thường.
Bạn có tò mò phép nhân ma trận thực hiện cụ thể như thế nào không? Hãy tìm kiếm các ví dụ chi tiết hoặc công cụ tính toán online để thực hành nhé!
Nhân ma trận với một số (vô hướng)
Phép toán này đơn giản: bạn chỉ cần nhân số đó với từng phần tử của ma trận.
Ứng Dụng “Thần Kỳ” Của Ma Trận Trong Đời Sống – Bạn Có Tin Không?
Đến đây, có lẽ bạn đã hiểu hơn về ma trận là gì và các phép toán liên quan. Nhưng điều thực sự làm nên sự “vi diệu” của ma trận chính là ứng dụng rộng rãi của nó.
Ứng dụng thực tế của ma trận trong nhiều lĩnh vực
Caption: Từ màn hình máy tính đến các mô hình kinh tế, dấu ấn của ma trận hiện diện ở khắp mọi nơi.
Giải hệ phương trình tuyến tính: “Vũ khí” lợi hại của toán học và kỹ thuật
Đây là ứng dụng kinh điển. Bất kỳ hệ phương trình tuyến tính nào cũng có thể được biểu diễn dưới dạng ma trận Ax = B, trong đó A là ma trận hệ số, x là vector các ẩn số, và B là vector các hằng số. Việc giải hệ phương trình trở thành việc tìm ma trận nghịch đảo hoặc sử dụng các phương pháp khử Gauss dựa trên ma trận. Làm sao để giải hệ phương trình bằng ma trận hiệu quả? Đây là kỹ năng cốt lõi trong nhiều ngành kỹ thuật đó!
Đồ họa máy tính và xử lý ảnh: Thế giới ảo được tạo nên từ ma trận?
- Biến đổi hình học: Mọi thao tác như xoay, phóng to, thu nhỏ, di chuyển đối tượng 2D, 3D đều được thực hiện thông qua phép nhân ma trận.
- Xử lý ảnh: Mỗi bức ảnh có thể xem là một ma trận các pixel. Các bộ lọc làm mờ, tăng độ nét,… thực chất là các phép toán trên ma trận điểm ảnh này.
Kinh tế lượng, phân tích dữ liệu: Ra quyết định dựa trên con số
- Mô hình Input-Output: Phân tích mối liên hệ giữa các ngành kinh tế.
- Phân tích hồi quy: Tìm mối quan hệ giữa các biến số.
- Khoa học dữ liệu: Ma trận là cấu trúc dữ liệu cơ bản để lưu trữ và xử lý thông tin khách hàng, sản phẩm, thị trường… Bạn có biết ma trận trong kinh tế giúp dự báo xu hướng thị trường không?
Lập trình và Khoa học máy tính: Từ thuật toán đến AI
- Biểu diễn đồ thị: Ma trận kề (adjacency matrix) dùng để biểu diễn các mối quan hệ trong mạng lưới (mạng xã hội, mạng máy tính).
- Thuật toán: Nhiều thuật toán tối ưu hóa, tìm đường đi ngắn nhất sử dụng ma trận.
- Trí tuệ nhân tạo (AI) và Học máy (Machine Learning): Ma trận là nền tảng của mạng nơ-ron (neural networks), các thuật toán xử lý ngôn ngữ tự nhiên, hệ gợi ý (recommendation systems)… Ma trận trong lập trình và AI là chìa khóa để xây dựng các hệ thống thông minh.
Các lĩnh vực khác: Mạng lưới, tối ưu hóa,…
Ma trận còn xuất hiện trong lý thuyết đồ thị, quy hoạch tuyến tính (tối ưu hóa tài nguyên), vật lý lượng tử, và nhiều ngành khoa học kỹ thuật khác.
Học Ma Trận: Thách Thức Hay Cơ Hội?
Việc tiếp cận ma trận ban đầu có thể hơi trừu tượng và đòi hỏi sự tỉ mỉ trong tính toán. Vậy học ma trận có khó không?
Những khó khăn thường gặp khi mới bắt đầu
- Tính trừu tượng: Khó hình dung ý nghĩa vật lý/thực tế của các phép toán.
- Tính toán phức tạp: Phép nhân ma trận hoặc tìm ma trận nghịch đảo có thể tốn nhiều bước và dễ sai sót nếu làm thủ công.
- Nhiều khái niệm liên quan: Định thức, hạng ma trận, trị riêng, vector riêng… cần thời gian để nắm vững.
Bí kíp chinh phục Ma trận hiệu quả
- Nắm vững định nghĩa và tính chất: Hiểu rõ bản chất trước khi đi vào tính toán.
- Thực hành thường xuyên: Làm bài tập từ cơ bản đến nâng cao. Không có cách nào tốt hơn để thành thạo là tự tay làm!
- Sử dụng công cụ hỗ trợ: Máy tính bỏ túi, phần mềm (MATLAB, Python với NumPy, Excel) có thể giúp kiểm tra kết quả và xử lý các ma trận lớn.
- Tìm kiếm ví dụ thực tế: Liên hệ kiến thức với các ứng dụng sẽ giúp bạn hiểu sâu và nhớ lâu hơn.
- Đừng ngại hỏi: Trao đổi với bạn bè, thầy cô hoặc tìm kiếm trên các diễn đàn, cộng đồng học thuật.
Nguồn tài liệu tham khảo uy tín
Bạn có thể tìm thấy rất nhiều tài liệu về ma trận trong sách giáo trình Đại số tuyến tính, các khóa học online (Coursera, edX, Khan Academy), và tất nhiên, đừng quên khám phá kho Tài Liệu Siêu Cấp về toán học và lập trình ngay tại Tailieusieucap.com nhé! Chúng mình luôn cập nhật những kiến thức hữu ích và bài tập thực hành đa dạng.
[internal_links]
Vậy, “Ma Trận” Mang Lại Cho Bạn Những Gì?
Việc hiểu và sử dụng thành thạo ma trận không chỉ giúp bạn vượt qua các môn học mà còn mang lại nhiều lợi ích thiết thực:
Người đang học và nghiên cứu về ma trận với biểu cảm tập trung và hứng thú
Caption: Đầu tư thời gian để hiểu về ma trận là đầu tư cho tư duy và tương lai của bạn.
Nền tảng kiến thức vững chắc
Ma trận là ngôn ngữ chung trong nhiều lĩnh vực khoa học, kỹ thuật, công nghệ và kinh tế. Nắm vững nó là bạn đã có một nền tảng quan trọng.
Tư duy logic và giải quyết vấn đề
Làm việc với ma trận rèn luyện khả năng tư duy cấu trúc, phân tích vấn đề một cách hệ thống và tìm ra giải pháp tối ưu.
Cơ hội nghề nghiệp rộng mở
Kiến thức về ma trận và đại số tuyến tính là yêu cầu cơ bản hoặc lợi thế lớn trong các ngành như Khoa học dữ liệu, Trí tuệ nhân tạo, Kỹ thuật phần mềm, Phân tích tài chính, Kỹ thuật điều khiển…
Kết Luận: Ma Trận – Chìa Khóa Mở Ra Nhiều Cánh Cửa
Như vậy, chúng ta đã cùng nhau đi qua một hành trình khám phá về ma trận. Hy vọng rằng, thay vì cảm thấy “đáng sợ”, giờ đây bạn đã thấy ma trận gần gũi, thú vị và cực kỳ hữu dụng. Nó không chỉ là những con số khô khan mà là một công cụ mạnh mẽ để mô tả thế giới, giải quyết vấn đề và tạo ra những công nghệ đột phá.
Đừng ngần ngại bắt đầu tìm hiểu sâu hơn về ma trận, dù mục tiêu của bạn là gì. Hãy xem nó như một thử thách để rèn luyện tư duy và một cơ hội để mở rộng kiến thức, nâng cao kỹ năng của bản thân.
Bạn thấy ứng dụng nào của ma trận là thú vị nhất? Bạn có câu hỏi nào khác về ma trận không? Hãy để lại bình luận bên dưới nhé! Đừng quên chia sẻ bài viết này nếu bạn thấy hữu ích và tiếp tục khám phá những Tài Liệu Siêu Cấp khác tại Tailieusieucap.com!