Bạn đã bao giờ tự hỏi, làm thế nào người ta biết được một bể bơi chứa bao nhiêu nước? Hay một chiếc hộp có thể đựng được bao nhiêu đồ? Hoặc đơn giản hơn, ly nước bạn đang cầm chứa bao nhiêu chất lỏng? Tất cả những câu hỏi đó đều xoay quanh một khái niệm quen thuộc nhưng đôi khi lại hơi “khó nhằn” – đó chính là Thể Tích.
Chào mừng bạn đến với Tailieusieucap.com! Hôm nay, chúng ta sẽ cùng nhau “mổ xẻ” mọi ngóc ngách về Thể Tích, từ những định nghĩa cơ bản nhất đến các công thức tính toán và ứng dụng thú vị trong cuộc sống. Đừng lo lắng nếu bạn thấy hơi “ngợp” nhé, mình sẽ dẫn dắt bạn đi từng bước thật dễ hiểu, như một cuộc trò chuyện thân mật vậy! Sẵn sàng chưa nào? Bắt đầu thôi!
Thể Tích Là Gì? Giải Mã Khái Niệm Quen Mà Lạ
Nghe “thể tích” có vẻ hơi học thuật, nhưng thực ra nó lại vô cùng gần gũi. Bạn có thể hình dung thế này…
Định nghĩa đơn giản, dễ hiểu
Thể tích (tiếng Anh: Volume) chính là lượng không gian mà một vật chiếm giữ. Hãy tưởng tượng bạn có một cục rubik, thể tích của nó chính là toàn bộ phần không gian mà cục rubik đó “chiếm chỗ”. Hay như ly nước mình vừa nhắc, thể tích nước trong ly là phần không gian mà nước lấp đầy bên trong ly.
Nói một cách khoa học hơn, thể tích là độ lớn của phần không gian ba chiều được giới hạn bởi một vật thể hoặc một bề mặt khép kín.
Phân biệt Thể Tích và Dung Tích: Đừng nhầm lẫn nhé!
Nhiều người hay nhầm lẫn giữa thể tích và dung tích (Capacity). Tuy có liên quan nhưng chúng không hoàn toàn giống nhau:
- Thể tích: Chỉ lượng không gian bên trong lẫn bên ngoài mà vật chiếm giữ (tính cả phần vỏ, vật liệu).
- Dung tích: Chỉ khả năng chứa đựng của một vật rỗng. Ví dụ, chai nước 1 lít có dung tích là 1 lít, nghĩa là nó có thể chứa được tối đa 1 lít nước. Thể tích của chai nước đó (tính cả phần nhựa) sẽ lớn hơn 1 lít một chút.
Dễ hình dung hơn, dung tích là “sức chứa”, còn thể tích là “phần không gian chiếm chỗ”.
Tại sao “Thể Tích” lại quan trọng đến vậy?
Hiểu về thể tích không chỉ để giải toán đâu nhé! Nó có vô vàn ứng dụng quan trọng:
- Trong đời sống: Tính lượng nước cần cho bể cá, lượng sơn cần để sơn nhà, dung tích tủ lạnh, sức chứa vali,…
- Trong khoa học & kỹ thuật: Tính toán trong xây dựng (bê tông, vật liệu), hóa học (pha chế dung dịch), vật lý (khí động học), y học (dung tích phổi),…
- Trong kinh doanh: Tính toán không gian kho hàng, chi phí vận chuyển dựa trên thể tích hàng hóa,…
Rõ ràng, nắm vững khái niệm thể tích giúp chúng ta giải quyết rất nhiều vấn đề thực tế, phải không nào?
Đơn Vị Đo Thể Tích: “Ngôn Ngữ” Của Không Gian
Để diễn tả “độ lớn” của không gian, chúng ta cần có đơn vị đo. Cũng giống như đo chiều dài dùng mét (m), đo khối lượng dùng kilogam (kg), thì đo thể tích cũng có những đơn vị riêng.
Các đơn vị phổ biến
- Mét khối (m³): Đây là đơn vị đo thể tích chuẩn trong Hệ đo lường quốc tế (SI). Một mét khối tương đương với thể tích của một hình lập phương có cạnh dài 1 mét. Đơn vị này thường dùng cho các vật thể lớn như bể nước, phòng ốc, container,…
- Đề-xi-mét khối (dm³): 1 dm³ = 0.001 m³. Thật thú vị, 1 dm³ = 1 Lít (L). Đây là mối liên hệ cực kỳ quan trọng!
- Xăng-ti-mét khối (cm³): 1 cm³ = 0.001 dm³ = 0.000001 m³. Đơn vị này thường dùng cho các vật nhỏ hơn. Đặc biệt, 1 cm³ = 1 mi-li-lít (mL).
- Lít (L) và Mi-li-lít (mL): Đây là các đơn vị rất thông dụng trong đời sống hàng ngày, thường dùng để đo thể tích chất lỏng (nước ngọt, sữa, xăng dầu,…).
Bảng quy đổi đơn vị đo thể tích
Caption: Các đơn vị đo thể tích phổ biến và mối liên hệ giữa chúng. Ghi nhớ 1 dm³ = 1L và 1 cm³ = 1mL sẽ rất hữu ích!
Mẹo chuyển đổi đơn vị nhanh chóng
Việc chuyển đổi giữa các đơn vị thể tích đôi khi hơi rối. Hãy nhớ quy tắc cơ bản sau:
- Khi chuyển từ đơn vị lớn sang đơn vị nhỏ liền kề (trong hệ mét khối): Nhân với 1000 (Ví dụ: 1 m³ = 1000 dm³; 1 dm³ = 1000 cm³).
- Khi chuyển từ đơn vị nhỏ sang đơn vị lớn liền kề: Chia cho 1000 (Ví dụ: 1000 cm³ = 1 dm³; 1000 dm³ = 1 m³).
- Ghi nhớ các mối liên hệ đặc biệt: 1 m³ = 1000 L; 1 L = 1000 mL; 1 dm³ = 1 L; 1 cm³ = 1 mL.
Tailieusieucap.com có các bài viết chi tiết hơn về cách quy đổi đơn vị, bạn có thể tìm đọc thêm nhé! [internal_links]
Bí Kíp Tính Thể Tích Các Hình Khối Cơ Bản (Công Thức & Ví Dụ)
Đây chắc chắn là phần mà nhiều bạn mong chờ nhất! Làm sao để tính được thể tích của các hình khối quen thuộc? Đừng lo, công thức không hề phức tạp đâu.
Thể tích Hình Hộp Chữ Nhật & Hình Lập Phương
Đây là hai dạng hình khối cơ bản và dễ tính nhất.
-
Hình Hộp Chữ Nhật: Có 3 kích thước là chiều dài (a), chiều rộng (b) và chiều cao (h).
Công thức:V = a x b x h
Ví dụ: Một bể cá hình hộp chữ nhật dài 1.2m, rộng 0.5m và cao 0.6m. Thể tích bể là: V = 1.2 x 0.5 x 0.6 = 0.36 m³. (Tức là bể chứa được 360 lít nước nếu đổ đầy). -
Hình Lập Phương: Là trường hợp đặc biệt của hình hộp chữ nhật khi cả 3 cạnh bằng nhau (cạnh a).
Công thức:V = a x a x a = a³
Ví dụ: Một viên xúc xắc hình lập phương có cạnh 2cm. Thể tích của nó là: V = 2 x 2 x 2 = 8 cm³.
Caption: Công thức tính thể tích hình hộp chữ nhật và hình lập phương – nền tảng cơ bản cần nắm vững.
Thể tích Hình Trụ
Hình trụ giống như lon sữa đặc hay ống nước vậy. Để tính thể tích, bạn cần biết bán kính đáy (r) và chiều cao (h).
Công thức: V = π x r² x h
(Trong đó, π (pi) là hằng số, xấp xỉ bằng 3.14159…)
Ví dụ: Một lon nước ngọt hình trụ có bán kính đáy 3cm và chiều cao 12cm. Thể tích lon nước là: V ≈ 3.14 x (3²) x 12 ≈ 3.14 x 9 x 12 ≈ 339.12 cm³ (khoảng 339 mL).
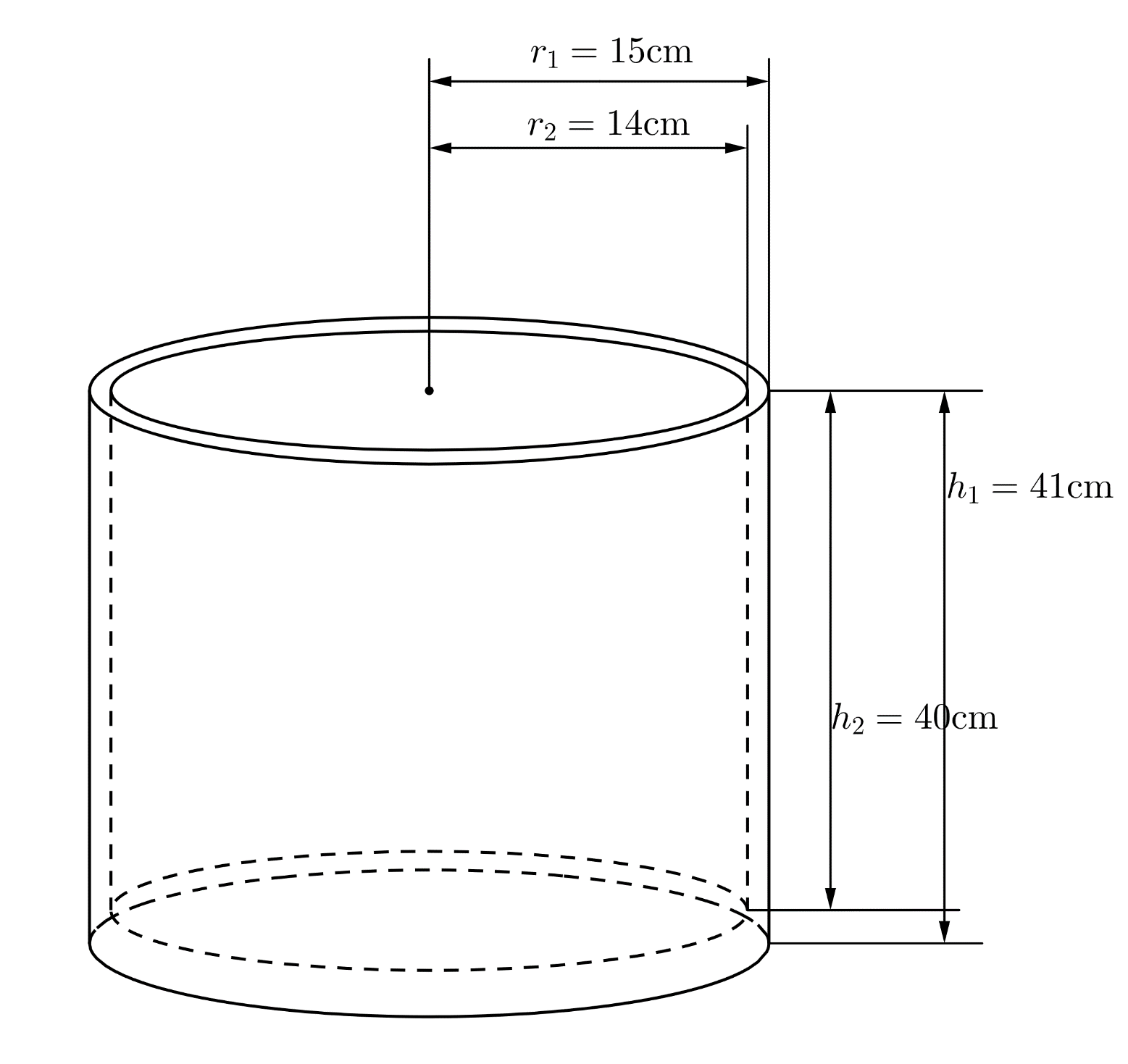Công thức tính thể tích hình trụ
Caption: Tính thể tích hình trụ dễ dàng với công thức V = πr²h. Đừng quên π ≈ 3.14 nhé!
Thể tích Hình Nón
Cây kem ốc quế hay chiếc nón lá là những ví dụ về hình nón. Bạn cũng cần bán kính đáy (r) và chiều cao (h) (là khoảng cách từ đỉnh nón đến tâm đáy).
Công thức: V = (1/3) x π x r² x h
(Lưu ý: Thể tích hình nón chỉ bằng 1/3 thể tích hình trụ có cùng bán kính đáy và chiều cao!)
Ví dụ: Một chiếc nón giấy hình nón có bán kính đáy 5cm và chiều cao 10cm. Thể tích của nó là: V = (1/3) x 3.14 x (5²) x 10 ≈ (1/3) x 3.14 x 25 x 10 ≈ 261.7 cm³.
Thể tích Hình Cầu
Quả bóng đá, viên bi là những hình cầu quen thuộc. Bạn chỉ cần biết bán kính (r) của nó.
Công thức: V = (4/3) x π x r³
Ví dụ: Một quả bóng chuyền có bán kính khoảng 10.5cm. Thể tích không khí bên trong quả bóng là: V = (4/3) x 3.14 x (10.5³) ≈ (4/3) x 3.14 x 1157.625 ≈ 4846.6 cm³.
Công thức tính thể tích hình cầu
Caption: Công thức tính thể tích hình cầu: V = (4/3)πr³. Chỉ cần biết bán kính là tính được ngay!
Lưu ý khi áp dụng công thức
- Đồng nhất đơn vị: Trước khi lắp số vào công thức, hãy đảm bảo tất cả các kích thước (chiều dài, rộng, cao, bán kính) đều ở cùng một đơn vị đo. Nếu chưa cùng đơn vị, bạn cần quy đổi chúng về cùng một đơn vị trước. Kết quả thể tích sẽ có đơn vị tương ứng (ví dụ: kích thước đo bằng cm thì thể tích là cm³).
- Đo đạc chính xác: Kết quả tính toán chỉ chính xác khi các số đo đầu vào chính xác.
- Sử dụng số Pi (π): Tùy yêu cầu bài toán hoặc độ chính xác mong muốn, bạn có thể dùng π ≈ 3.14, π ≈ 3.1416 hoặc giữ nguyên ký hiệu π trong kết quả.
“Thể Tích” Trong Đời Sống: Không Chỉ Là Công Thức Sách Vở
Bạn có nhận ra thể tích hiện diện xung quanh chúng ta không?
Ứng dụng thực tế thú vị
- Nấu ăn & Pha chế: Đo lường thể tích nguyên liệu (sữa, nước, dầu ăn, bột…) bằng cốc đong, thìa đo là ứng dụng trực tiếp. Các công thức nấu ăn chính là sự kết hợp thể tích các thành phần đấy!
- Xây dựng & Kiến trúc: Tính toán lượng bê tông cần đổ móng, lượng đất cần đào, thể tích không gian phòng để lắp điều hòa phù hợp,… đều cần đến thể tích.
- Vận chuyển & Logistics: Phí vận chuyển hàng hóa thường được tính dựa trên trọng lượng hoặc thể tích quy đổi (đặc biệt với hàng cồng kềnh). Sắp xếp hàng hóa trong container sao cho tối ưu không gian cũng là bài toán về thể tích.
- Nông nghiệp: Tính toán lượng nước tưới tiêu cho một diện tích đất trồng.
- Y tế: Đo dung tích sống của phổi, tính liều lượng thuốc dạng lỏng,…
Làm sao đo thể tích vật không đều? Bật mí phương pháp Archimedes!
Với những vật có hình dạng phức tạp, không theo khuôn mẫu nào (như hòn đá, củ khoai tây), làm sao để đo thể tích? Có một cách rất hay dựa trên nguyên lý của nhà bác học Archimedes: phương pháp dùng bình tràn (hoặc cốc chia độ).
- Đổ một lượng nước vừa đủ vào bình chia độ, ghi lại mực nước ban đầu (V1).
- Nhúng chìm hoàn toàn vật cần đo vào bình nước. Đảm bảo nước không tràn ra ngoài (nếu dùng cốc chia độ) hoặc hứng phần nước tràn ra (nếu dùng bình tràn).
- Ghi lại mực nước lúc sau (V2) hoặc đo thể tích phần nước tràn ra (Vt).
- Thể tích của vật chính là độ tăng thể tích của nước trong bình: V_vật = V2 – V1 (hoặc bằng thể tích nước tràn ra V_vật = Vt).
Thật đơn giản mà hiệu quả, đúng không?
Câu Hỏi Thường Gặp Về Thể Tích (Giải Đáp Nhanh)
Trong quá trình tìm hiểu về thể tích, có thể bạn sẽ gặp một số thắc mắc. Tailieusieucap.com đã tổng hợp và giải đáp nhanh một vài câu hỏi phổ biến:
- Thể tích có thể âm không?
- Trong toán học và vật lý thông thường, thể tích của một vật thể thực luôn là một giá trị dương hoặc bằng 0 (với vật thể có kích thước không đáng kể). Khái niệm “thể tích âm” đôi khi xuất hiện trong các ngữ cảnh toán học trừu tượng hơn, nhưng không áp dụng cho không gian vật lý thông thường.
- Làm sao tính thể tích vật rỗng? (Ví dụ: hộp rỗng)
- Bạn cần tính thể tích bên ngoài của vật (coi như đặc) rồi trừ đi thể tích phần rỗng bên trong. Ví dụ, với hộp gỗ rỗng, bạn tính thể tích khối gỗ bên ngoài, rồi tính thể tích khoảng không bên trong, sau đó lấy thể tích ngoài trừ thể tích trong để ra thể tích phần gỗ.
- Đơn vị thể tích nào được dùng nhiều nhất?
- Tùy thuộc vào lĩnh vực. Trong đời sống hàng ngày, Lít (L) và Mi-li-lít (mL) rất phổ biến cho chất lỏng. Trong khoa học và kỹ thuật, mét khối (m³) và các đơn vị dẫn xuất (cm³, dm³) được dùng nhiều hơn.
- Tính thể tích khí như thế nào?
- Thể tích của chất khí chính là thể tích của vật chứa nó. Ví dụ, thể tích không khí trong một căn phòng chính là thể tích của căn phòng đó.
Bạn còn câu hỏi nào khác về thể tích không? Đừng ngần ngại để lại bình luận bên dưới nhé!
Làm Thế Nào Để Giỏi Hơn Về “Thể Tích”? (Cách Thực Hiện)
Nắm vững kiến thức về thể tích không khó nếu bạn có phương pháp đúng:
Thực hành thường xuyên
- Giải bài tập: Cách tốt nhất để nhớ công thức và hiểu bản chất là làm bài tập, từ cơ bản đến nâng cao. Tìm các bài toán tính thể tích hình khối trong sách giáo khoa, sách tham khảo hoặc trên mạng.
- Sử dụng công cụ online: Có rất nhiều website (bao gồm cả Tailieusieucap.com) cung cấp công cụ tính thể tích online. Hãy thử nhập kích thước và kiểm tra kết quả. [internal_links]
Liên hệ thực tế
- Quan sát xung quanh: Tập ước lượng thể tích các vật dụng hàng ngày: hộp sữa, chai nước, phòng học, bể cá… Sau đó thử đo đạc và tính toán để so sánh.
- Thực hiện thí nghiệm: Thử đo thể tích vật không đều bằng phương pháp bình tràn như đã hướng dẫn.
Tìm hiểu sâu hơn
- Đọc thêm tài liệu: Tìm hiểu về các hình khối phức tạp hơn, các phương pháp tính thể tích nâng cao (ví dụ: tích phân trong toán học).
- Khám phá ứng dụng: Tìm hiểu xem thể tích được ứng dụng cụ thể như thế nào trong các ngành nghề bạn quan tâm (kiến trúc, kỹ thuật, hóa học…).
Kiên trì luyện tập và liên hệ thực tế, bạn sẽ thấy thể tích không còn là khái niệm khô khan nữa!
Ý Nghĩa Của Việc Nắm Vững Khái Niệm “Thể Tích”
Hiểu và tính toán được thể tích mang lại cho bạn nhiều lợi ích hơn bạn nghĩ:
- Kiến thức nền tảng vững chắc: Thể tích là một phần quan trọng của hình học không gian, là nền tảng cho nhiều môn khoa học tự nhiên và kỹ thuật khác.
- Kỹ năng giải quyết vấn đề: Việc tính toán thể tích rèn luyện tư duy logic, khả năng phân tích và áp dụng công thức vào tình huống cụ thể.
- Ứng dụng thực tiễn cao: Giúp bạn tự tin hơn khi giải quyết các vấn đề liên quan đến không gian, sức chứa trong cuộc sống hàng ngày và công việc.
- Phát triển tư duy không gian: Hình dung và làm việc với các vật thể ba chiều giúp cải thiện khả năng cảm nhận không gian của bạn.
Kết Luận: “Thể Tích” – Chìa Khóa Mở Cánh Cửa Không Gian
Vậy là chúng ta đã cùng nhau đi qua một hành trình khám phá khá đầy đủ về thể tích – từ định nghĩa, đơn vị đo, các công thức tính toán cơ bản đến những ứng dụng thực tế thú vị. Hy vọng rằng, qua bài viết này của Tailieusieucap.com, khái niệm “thể tích” đã trở nên gần gũi và dễ hiểu hơn với bạn.
Hãy nhớ rằng, thể tích không chỉ là những con số và công thức khô khan, mà nó ẩn chứa cách chúng ta đo lường và tương tác với thế giới không gian ba chiều xung quanh. Việc nắm vững kiến thức này sẽ là một công cụ hữu ích, giúp bạn giải quyết nhiều vấn đề trong học tập và cuộc sống.
Đừng quên thực hành thường xuyên và quan sát thế giới xung quanh để thấy thể tích hiện diện ở khắp mọi nơi nhé!
Bạn thấy bài viết này hữu ích chứ? Bạn có mẹo hay công thức tính thể tích nào muốn chia sẻ không? Hãy để lại bình luận bên dưới, chúng ta cùng thảo luận thêm nhé! Và đừng quên chia sẻ bài viết này đến bạn bè nếu bạn thấy nó có giá trị!
Khám phá thêm nhiều tài liệu và kiến thức bổ ích khác tại Tailieusieucap.com! [internal_links]
Lưu ý: Nội dung bài viết mang tính chất tham khảo, cung cấp kiến thức về khái niệm thể tích trong toán học và ứng dụng thực tế. Tailieusieucap.com luôn đề cao tính chính xác và trung thực của thông tin, không cổ súy các hành vi vi phạm pháp luật hay mê tín dị đoan.