Tích Phân Bất Định: Chìa Khóa Vàng Mở Cánh Cửa Giải Tích Hay Chỉ Là “Cơn Ác Mộng”?

Tháng 5 5, 2025 Lớp 12

Chào bạn, có phải bạn đang cảm thấy hơi “choáng” khi nghe đến hai từ Tích Phân Bất định? Hay bạn đang loay hoay tìm cách giải những bài tập tích phân khiến đầu óc quay cuồng? Đừng lo lắng, bạn không hề đơn độc! Rất nhiều người khi mới bắt đầu học Giải tích cũng từng có cảm giác như vậy.

Hãy tưởng tượng thế này: Bạn biết cách một cái cây lớn lên mỗi ngày (đó là tốc độ tăng trưởng – giống như đạo hàm). Vậy làm sao để từ tốc độ đó, bạn tìm lại được chiều cao ban đầu của cái cây tại một thời điểm bất kỳ? Đó chính là lúc Tích Phân Bất định xuất hiện như một “phép màu ngược”, giúp chúng ta tìm lại hàm số gốc từ đạo hàm của nó.

Nghe có vẻ thú vị đúng không? Trong bài viết này, chúng ta sẽ cùng nhau đi từ A đến Z, khám phá mọi ngóc ngách của tích phân bất định, từ định nghĩa cơ bản đến các phương pháp tính toán hiệu quả và cả những ứng dụng thực tế của nó nữa. Cùng bắt đầu hành trình này nhé!

Tích phân bất định là gì? Giải mã khái niệm cốt lõi

Okay, vào thẳng vấn đề luôn nhé! Hiểu đơn giản nhất, Tích phân bất định của một hàm số f(x) là quá trình tìm một hàm số F(x) sao cho đạo hàm của F(x) chính là f(x). Nghe quen quen phải không nào? Nó chính là phép toán ngược của phép lấy đạo hàm mà bạn đã học đấy!

Mối liên hệ “ngược đời” với đạo hàm

Người ta thường gọi F(x) là nguyên hàm của f(x). Nếu F'(x) = f(x) thì ∫f(x)dx = F(x) + C.

Khám Phá “Không Gian”: Từ Vũ Trụ Bao La Đến Góc Nhỏ Thân Thương Của Bạn
  • f(x): Hàm số dưới dấu tích phân.
  • F(x): Một nguyên hàm của f(x).
  • ∫: Ký hiệu tích phân.
  • dx: Vi phân của biến số x, cho biết ta đang lấy tích phân theo biến nào.
  • C: Hằng số tích phân (sẽ giải thích ngay dưới đây).

Mối quan hệ này là nền tảng của toàn bộ lý thuyết tích phân. Biết đạo hàm, bạn có thể tìm được hàm số gốc (sai khác một hằng số).

Tại sao lại có hằng số C “bí ẩn”?

Bạn có bao giờ thắc mắc tại sao kết quả của tích phân bất định luôn có thêm “+ C” ở cuối không?

Lý do rất đơn giản: Đạo hàm của một hằng số luôn bằng 0.

Hình Elip: Bí Mật Đằng Sau Đường Cong Hoàn Hảo & Ứng Dụng Không Ngờ

Ví dụ nhé:

  • Đạo hàm của x² là 2x.
  • Đạo hàm của x² + 5 cũng là 2x.
  • Đạo hàm của x² - 100 vẫn là 2x.

Như vậy, có vô số hàm số (ví dụ: x², x² + 5, x² - 100,…) mà đạo hàm của chúng đều bằng 2x. Tất cả các hàm này chỉ khác nhau một hằng số. Do đó, khi tìm nguyên hàm của 2x, chúng ta không thể biết chính xác hàm số gốc là hàm nào, nên ta viết kết quả tổng quát là x² + C, trong đó C là một hằng số bất kỳ (Constant).

Vậy, tích phân bất định không cho ta một hàm số duy nhất, mà là một họ các hàm số song song với nhau trên đồ thị.

Ký hiệu và cách đọc

Ký hiệu ∫f(x)dx được đọc là “tích phân bất định của f(x) theo x”. Nó biểu thị cho tập hợp tất cả các nguyên hàm của hàm số f(x).

Hệ Tọa Độ: Từ Lý Thuyết Đến Thực Tế – Giải Mã Ngôn Ngữ Định Vị Vạn Vật

Bảng công thức Tích phân bất định cơ bản – “Bảo bối” không thể thiếu

Giống như bảng cửu chương khi học nhân chia, để chinh phục tích phân bất định, bạn cần nắm vững bảng công thức nguyên hàm cơ bản. Đây là những viên gạch đầu tiên xây dựng nên nền tảng kiến thức của bạn.

Dưới đây là một số công thức thông dụng nhất:

  • ∫k dx = kx + C (với k là hằng số)
  • ∫xⁿ dx = (xⁿ⁺¹ / (n+1)) + C (với n ≠ -1)
  • ∫(1/x) dx = ln|x| + C
  • ∫eˣ dx = eˣ + C
  • ∫aˣ dx = (aˣ / ln a) + C (với 0 < a ≠ 1)
  • ∫cos x dx = sin x + C
  • ∫sin x dx = -cos x + C
  • ∫(1/cos²x) dx = tan x + C
  • ∫(1/sin²x) dx = -cot x + C
  • … (và nhiều công thức khác cho hàm lượng giác ngược, hypebol,…)

Mẹo nhỏ: Cách tốt nhất để nhớ các công thức này là làm thật nhiều bài tập và liên hệ ngược lại với công thức đạo hàm tương ứng. Ví dụ, bạn biết đạo hàm của sin x là cos x, vậy nguyên hàm của cos x chính là sin x + C.

Bảng công thức tích phân bất định cơ bảnBảng công thức tích phân bất định cơ bản

Phương Là Gì? Giải Mã Từ Khóa Đa Nghĩa: Định Hướng, Phương Pháp và Hơn Thế Nữa

Caption: Bảng công thức tích phân bất định cơ bản là công cụ không thể thiếu khi giải toán. Hãy ghi nhớ hoặc để nó ở nơi dễ thấy bạn nhé!

Các tính chất quan trọng của Tích phân bất định

Để việc tính toán trở nên dễ dàng hơn, tích phân bất định có một số tính chất quan trọng bạn cần nắm:

  1. Tính chất tuyến tính:

    • ∫[f(x) + g(x)] dx = ∫f(x) dx + ∫g(x) dx (Tích phân của tổng bằng tổng các tích phân)
    • ∫[f(x) – g(x)] dx = ∫f(x) dx – ∫g(x) dx (Tích phân của hiệu bằng hiệu các tích phân)
    • ∫k f(x) dx = k ∫f(x) dx (Hằng số k có thể đưa ra ngoài dấu tích phân)

  2. (∫f(x) dx)’ = f(x): Đạo hàm của tích phân bất định chính là hàm số dưới dấu tích phân.

Những tính chất này giúp chúng ta “chẻ nhỏ” các bài toán tích phân phức tạp thành những bài toán đơn giản hơn, có thể áp dụng trực tiếp công thức cơ bản.

Các phương pháp tính Tích phân bất định hiệu quả

Không phải lúc nào chúng ta cũng gặp những bài tích phân có thể áp dụng ngay công thức cơ bản. Đó là lúc các phương pháp tính tích phân phát huy tác dụng. Hai phương pháp phổ biến nhất là:

Phương pháp đổi biến số – “Biến hình” bài toán

Đây là phương pháp cực kỳ mạnh mẽ, giúp đưa một tích phân phức tạp về dạng đơn giản hơn mà chúng ta đã biết cách giải. Ý tưởng chính là đặt một biểu thức trong hàm dưới dấu tích phân bằng một biến mới (thường là u hoặc t).

Phép Đồng Biến: Giải Mã “Người Bạn Đồng Hành” Cùng Chiều Trong Toán Học!

Khi nào nên dùng?

  • Khi dưới dấu tích phân có dạng f(g(x)) * g'(x). Ta sẽ đặt u = g(x), khi đó du = g'(x)dx. Tích phân ban đầu trở thành ∫f(u)du, thường dễ giải hơn nhiều.
  • Khi bạn thấy một biểu thức và đạo hàm của nó cùng xuất hiện (sai khác hằng số).

Ví dụ: Tính ∫2x * (x² + 1)⁵ dx

  • Nhận thấy (x² + 1)' = 2x. Quá tuyệt vời!
  • Đặt u = x² + 1 => du = 2x dx.
  • Tích phân trở thành: ∫u⁵ du = (u⁶ / 6) + C
  • Thay u trở lại: ( (x² + 1)⁶ / 6 ) + C
**Hình Hyperbol: Khám Phá Đường Cong Kỳ Diệu Từ A Đến Z | Tailieusieucap.com**

Phương pháp tích phân từng phần – Khi “tích” trở nên phức tạp

Phương pháp này dựa trên công thức đạo hàm của một tích: (uv)' = u'v + uv'. Lấy tích phân hai vế, ta có công thức tích phân từng phần:

∫u dv = uv – ∫v du

Khi nào nên dùng?

  • Khi hàm dưới dấu tích phân là tích của hai loại hàm khác nhau (ví dụ: đa thức lượng giác, đa thức mũ, mũ lượng giác, đa thức logarit,…).
  • Mục tiêu là chọn u và dv sao cho tích phân ∫v du ở vế phải đơn giản hơn tích phân ban đầu ∫u dv.

Mẹo chọn u và dv (Quy tắc LIATE hoặc ILATE): Ưu tiên chọn u theo thứ tự:

  • Logarit (ln x, log x)
  • Inverse Trigonometric (arcsin x, arccos x, arctan x)
  • Algebraic (đa thức: x², 3x+5,…)
  • Trigonometric (sin x, cos x,…)
  • Exponential (eˣ, aˣ)
Số Thực Là Gì? Giải Mã Toàn Tập Khái Niệm Nền Tảng Của Toán Học

Phần còn lại (bao gồm cả dx) sẽ là dv.

Ví dụ: Tính ∫x * eˣ dx

  • Theo quy tắc LIATE, chọn u = x (Algebraic) và dv = eˣ dx (Exponential).
  • Suy ra: du = dx và v = ∫eˣ dx = eˣ.
  • Áp dụng công thức: ∫x eˣ dx = x eˣ – ∫eˣ dx = x * eˣ – eˣ + C

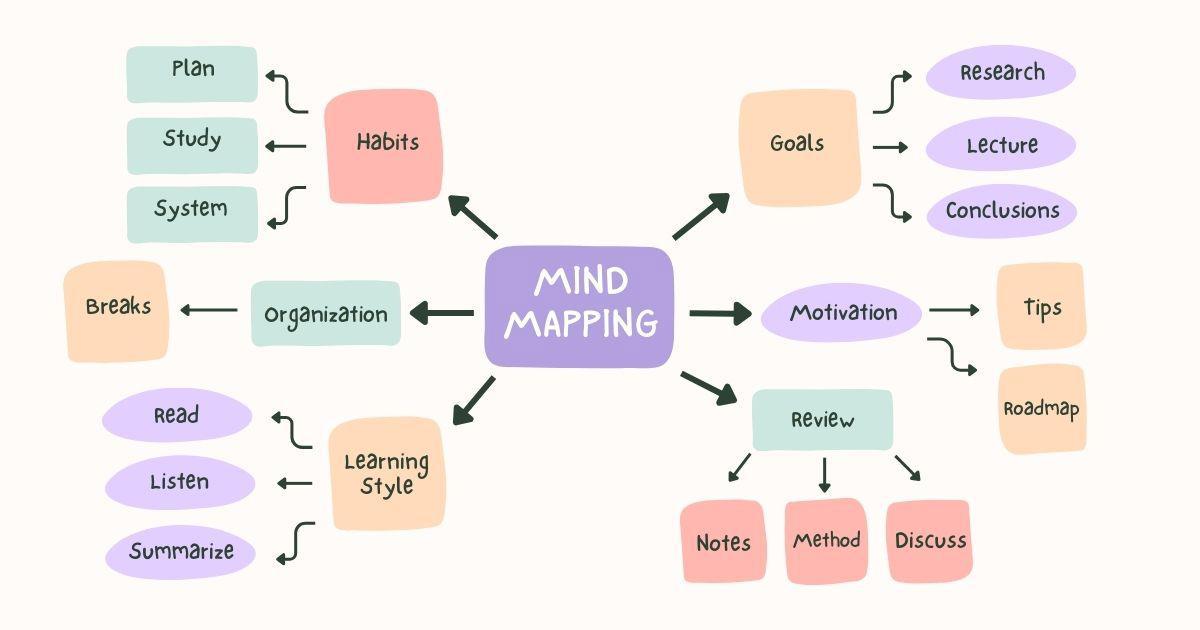Sơ đồ tư duy các phương pháp tính tích phân bất địnhSơ đồ tư duy các phương pháp tính tích phân bất định

Ma Trận Là Gì? Giải Mã Toàn Tập Khái Niệm & Ứng Dụng Thực Tế 2024

Caption: Gặp bài toán tích phân bất định khó? Sơ đồ này giúp bạn định hướng phương pháp giải phù hợp.

Những “cạm bẫy” thường gặp khi tính Tích phân bất định

Hành trình chinh phục tích phân không phải lúc nào cũng trải hoa hồng. Dưới đây là vài “ổ gà” mà bạn cần tránh:

  1. Quên hằng số C: Đây là lỗi kinh điển nhất! Luôn nhớ cộng + C vào cuối kết quả của tích phân bất định. Mất điểm vì lỗi này thì tiếc lắm đó!
  2. Áp dụng sai công thức: Nhầm lẫn giữa các công thức hoặc áp dụng công thức trong trường hợp không được phép (ví dụ: áp dụng công thức ∫xⁿ dx cho n = -1).
  3. Sai lầm khi đổi biến: Tính sai du hoặc quên thay đổi cận (trong tích phân xác định – sẽ nói ở bài khác) hoặc quên đổi biến trở lại hàm ban đầu sau khi tính xong.
  4. Sai lầm khi tích phân từng phần: Chọn u và dv không hợp lý khiến tích phân mới phức tạp hơn, hoặc tính sai v từ dv, tính sai du từ u.
  5. Tích phân của thương ≠ Thương các tích phân: Nhớ kỹ: ∫[f(x) / g(x)] dx KHÔNG bằng [∫f(x) dx] / [∫g(x) dx]. Tương tự với tích phân của tích.

Để tránh những lỗi này, cách duy nhất là luyện tập thật nhiều và luôn cẩn thận kiểm tra lại từng bước tính toán.

Câu hỏi thường gặp về Tích phân bất định (FAQ)

Trong quá trình tìm hiểu, chắc hẳn bạn sẽ có những thắc mắc. Dưới đây là một vài câu hỏi phổ biến:

  • Hỏi: Tích phân bất định và nguyên hàm có giống nhau không?

    • Đáp: Về bản chất, chúng rất giống nhau. Tích phân bất định ∫f(x)dx là ký hiệu cho tập hợp tất cả các nguyên hàm của f(x), tức là F(x) + C. Còn nguyên hàm F(x) chỉ là một hàm số cụ thể mà đạo hàm của nó bằng f(x). Trong nhiều trường hợp, người ta dùng hai thuật ngữ này thay thế cho nhau.

  • Hỏi: Làm sao để nhớ hết công thức tích phân?

    • Đáp: Không cần phải “nhớ vẹt”. Hãy hiểu mối liên hệ giữa đạo hàm và nguyên hàm. Luyện tập thường xuyên qua các bài tập từ cơ bản đến nâng cao sẽ giúp bạn tự động ghi nhớ và áp dụng công thức một cách thành thạo. Sử dụng flashcards hoặc mindmaps cũng là cách hay.

  • Hỏi: Khi nào dùng đổi biến, khi nào dùng từng phần?

    • Đáp: Như đã đề cập ở trên, hãy quan sát dạng của hàm số dưới dấu tích phân. Nếu thấy cấu trúc f(g(x)) * g'(x), hãy nghĩ đến đổi biến. Nếu thấy tích của hai loại hàm khác nhau (đa thức, logarit, mũ, lượng giác,…), hãy nghĩ đến tích phân từng phần và áp dụng quy tắc LIATE/ILATE để chọn u và dv. Đôi khi, bạn cần kết hợp cả hai phương pháp.

  • Hỏi: Tích phân bất định dùng để làm gì trong thực tế?

    • Đáp: Ồ, rất nhiều! Nó là nền tảng để tính tích phân xác định (dùng để tính diện tích, thể tích, độ dài cung,…). Nó còn là công cụ không thể thiếu để giải phương trình vi phân – loại phương trình mô tả rất nhiều hiện tượng trong vật lý (chuyển động, điện học), hóa học (tốc độ phản ứng), sinh học (tăng trưởng quần thể), kinh tế (mô hình tăng trưởng),…

Ý nghĩa và Ứng dụng của Tích phân bất định – Không chỉ là lý thuyết suông!

Bạn có nghĩ rằng học tích phân bất định chỉ để giải những bài toán trên giấy? Hoàn toàn không phải vậy! Khái niệm này có ý nghĩa và ứng dụng vô cùng to lớn:

  1. Nền tảng cho Tích phân Xác định: Hiểu và tính được tích phân bất định là điều kiện tiên quyết để bạn có thể tính tích phân xác định – công cụ dùng để tính diện tích hình phẳng giới hạn bởi các đường cong, thể tích vật thể tròn xoay, công của lực biến đổi, và nhiều đại lượng vật lý khác.
  2. Giải Phương trình Vi phân: Rất nhiều quy luật tự nhiên và xã hội được mô tả bằng phương trình vi phân (phương trình chứa đạo hàm). Để tìm nghiệm của các phương trình này, kỹ năng tìm nguyên hàm (tính tích phân bất định) là bắt buộc. Ví dụ: tìm phương trình chuyển động của vật từ gia tốc, dự đoán dân số từ tốc độ tăng trưởng,…
  3. Trong Kinh tế học: Tính thặng dư của nhà sản xuất, thặng dư của người tiêu dùng,…
  4. Trong Xác suất Thống kê: Tìm hàm phân phối xác suất từ hàm mật độ xác suất.

Hiểu được tích phân bất định không chỉ giúp bạn vượt qua các kỳ thi mà còn mở ra cánh cửa để hiểu sâu sắc hơn về thế giới xung quanh qua lăng kính Toán học. Đó là kiến thức, là tư duy logic, là nền tảng cho nhiều ngành khoa học và kỹ thuật.

Caption: Tích phân không chỉ nằm trên sách vở, nó hiện hữu trong việc mô tả chuyển động, tính toán trong kỹ thuật và nhiều lĩnh vực khác của đời sống.

[internal_links]

Kết luận

Vậy là chúng ta đã cùng nhau đi qua những khái niệm cơ bản nhất về Tích phân bất định. Hy vọng rằng qua bài viết này, bạn đã không còn cảm thấy sợ hãi mà thay vào đó là sự hứng thú và tự tin hơn khi đối mặt với “anh bạn” này.

Hãy nhớ rằng, tích phân bất định chính là phép toán ngược của đạo hàm, luôn đi kèm với hằng số C “bí ẩn” nhưng đầy ý nghĩa. Nắm vững bảng công thức cơ bản và các phương pháp tính toán như đổi biến số, tích phân từng phần là chìa khóa để bạn chinh phục mọi bài toán. Đừng quên luyện tập thường xuyên và tránh những lỗi sai phổ biến nhé!

Toán học, đặc biệt là Giải tích, giống như một trò chơi xếp hình khổng lồ. Tích phân bất định là một mảnh ghép quan trọng không thể thiếu. Hãy kiên nhẫn, tìm tòi và bạn sẽ thấy vẻ đẹp logic đằng sau những công thức tưởng chừng khô khan.

Bạn có gặp khó khăn gì khi học Tích phân bất định? Hay bạn có mẹo học tập nào muốn chia sẻ? Đừng ngần ngại để lại bình luận bên dưới nhé! Tailieusieucap.com luôn sẵn sàng lắng nghe và đồng hành cùng bạn trên con đường chinh phục kiến thức. Nếu thấy bài viết hữu ích, hãy chia sẻ cho bạn bè cùng biết nha!