Bạn đã bao giờ nghe đến “Hàm Số” và cảm thấy hơi… “lùng bùng lỗ tai” chưa? Hay bạn đang vật lộn với các bài tập về tập xác định, đồ thị, tính đơn điệu của Hàm Số? Đừng lo lắng, bạn không hề đơn độc đâu! Rất nhiều người khi mới tiếp cận Toán học cấp 3 hay thậm chí là đại học cũng từng cảm thấy hàm số là một khái niệm khá trừu tượng và khó nhằn.
Nhưng tin mình đi, hàm số thực ra lại là một người bạn đồng hành cực kỳ thú vị và quyền năng trong thế giới Toán học đấy! Nó giống như một “cỗ máy” biến đổi, một quy tắc diệu kỳ giúp chúng ta mô tả mối quan hệ giữa các đại lượng trong vô vàn lĩnh vực khác nhau.
Trong bài viết này, chúng ta sẽ cùng nhau “giải mã” hàm số một cách thật gần gũi, dễ hiểu, từ những khái niệm cơ bản nhất đến những ứng dụng không ngờ của nó trong cuộc sống. Hãy chuẩn bị sẵn sàng tinh thần khám phá nhé!
Hàm số là gì mà “ám ảnh” học sinh đến vậy?
Okay, thẳng thắn mà nói, định nghĩa sách giáo khoa đôi khi làm chúng ta hơi “choáng”. Nhưng đừng sợ, mình sẽ diễn giải lại theo cách dễ hiểu hơn.
Định nghĩa “chuẩn cơm mẹ nấu”
Hãy tưởng tượng hàm số giống như một cái máy chế biến đặc biệt. Bạn bỏ “nguyên liệu” đầu vào (gọi là biến số độc lập, thường ký hiệu là x), cái máy này (chính là quy tắc hàm số, thường ký hiệu là f) sẽ xử lý theo một công thức nhất định và cho ra “thành phẩm” đầu ra duy nhất (gọi là giá trị của hàm số tại x, hay biến số phụ thuộc, thường ký hiệu là y hoặc f(x)).
Điều cốt lõi nhất: Cứ một giá trị x hợp lệ đưa vào, chỉ cho ra một và chỉ một giá trị y tương ứng. Giống như bạn bấm nút “cà phê đen” trên máy pha tự động, nó chỉ cho ra cà phê đen chứ không thể vừa là cà phê đen vừa là trà sữa được!
Ví dụ đơn giản: Xét hàm số y = f(x) = 2x + 1.
- Nếu bạn cho x = 1 vào “máy”, nó sẽ tính 2*1 + 1 = 3. Vậy f(1) = 3.
- Nếu bạn cho x = 5 vào “máy”, nó sẽ tính 2*5 + 1 = 11. Vậy f(5) = 11.
 Sơ đồ minh họa hàm số như một cỗ máy
Sơ đồ minh họa hàm số như một cỗ máy
Caption: Hình dung hàm số như một cỗ máy: bỏ ‘x’ vào, nhận lại duy nhất ‘y = f(x)’.
Tập xác định và Tập giá trị: “Sân chơi” của hàm số
Nghe có vẻ học thuật nhỉ? Nhưng thực ra lại rất đơn giản:
- Tập xác định (TXĐ – Domain): Là tập hợp tất cả các giá trị x (nguyên liệu) mà bạn được phép bỏ vào “máy hàm số” để nó hoạt động được (không bị lỗi, không bị vô nghĩa).
- Ví dụ: Với hàm số y = 1/x, bạn không thể cho x = 0 vào được (vì không thể chia cho 0). Vậy TXĐ là tất cả các số thực khác 0. Ký hiệu: D = R {0}.
- Câu hỏi thường gặp: Làm sao để tìm tập xác định của hàm số? -> Bạn cần xem xét các điều kiện để hàm số có nghĩa: mẫu số khác 0, biểu thức trong căn bậc hai lớn hơn hoặc bằng 0, biểu thức trong logarit lớn hơn 0,…
- Tập giá trị (TGT – Range): Là tập hợp tất cả các giá trị y (thành phẩm) mà “máy hàm số” có thể tạo ra được từ những giá trị x hợp lệ trong tập xác định.
- Ví dụ: Với hàm số y = x², dù bạn cho x là số âm hay dương, thì y luôn luôn lớn hơn hoặc bằng 0. Vậy TGT là [0, +∞).
Hiểu rõ TXĐ và TGT giúp chúng ta biết được “phạm vi hoạt động” và “khả năng tạo ra kết quả” của một hàm số cụ thể.
Khám phá thế giới đa dạng của các loại hàm số
Hàm số không chỉ có một dạng đâu nhé! Có rất nhiều “thành viên” trong gia đình hàm số, mỗi loại lại có “tính cách” và “hình dáng” (đồ thị) riêng:
Các “gương mặt” quen thuộc
- Hàm số bậc nhất (Linear Function): Có dạng y = ax + b (với a ≠ 0). Đồ thị của nó luôn là một đường thẳng. Quen thuộc quá phải không? Ví dụ: Tính tiền taxi dựa trên số km đi được.
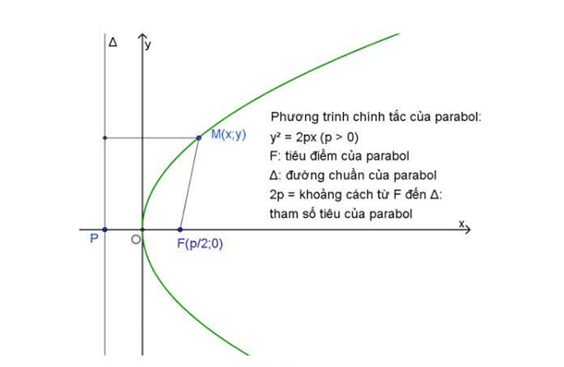
- Hàm số bậc hai (Quadratic Function): Có dạng y = ax² + bx + c (với a ≠ 0). Đồ thị là một đường cong Parabol cong cong, mềm mại. Ví dụ: Mô tả quỹ đạo của một vật được ném lên.
- Hàm số mũ và Logarit (Exponential & Logarithmic Functions): y = aˣ và y = logₐx. Hai hàm số này thường đi đôi với nhau, mô tả sự tăng trưởng hoặc suy giảm rất nhanh. Ví dụ: Lãi suất kép trong ngân hàng, sự phân rã phóng xạ.
- Hàm số lượng giác (Trigonometric Functions): y = sinx, y = cosx, y = tanx, y = cotx. Những hàm số này có tính tuần hoàn, lặp đi lặp lại, gắn liền với các góc và đường tròn. Ví dụ: Mô tả các dao động, sóng (sóng âm, sóng ánh sáng).
 Đồ thị của các loại hàm số cơ bản
Đồ thị của các loại hàm số cơ bản
Caption: Mỗi loại hàm số lại có một “dáng vẻ” đồ thị đặc trưng riêng.
Các “tính cách” đặc biệt
Ngoài “hình dáng”, hàm số còn có những “tính cách” hay đặc điểm riêng:
- Hàm số đồng biến (Increasing Function): Khi x tăng thì y cũng tăng theo. Đồ thị có xu hướng đi lên từ trái sang phải.
- Hàm số nghịch biến (Decreasing Function): Khi x tăng thì y lại giảm. Đồ thị có xu hướng đi xuống từ trái sang phải.
- Hàm số chẵn (Even Function): Đồ thị đối xứng qua trục tung Oy (giống như soi gương qua trục Oy). Có tính chất f(-x) = f(x). Ví dụ: y = x².
- Hàm số lẻ (Odd Function): Đồ thị đối xứng qua gốc tọa độ O. Có tính chất f(-x) = -f(x). Ví dụ: y = x³.
Việc xác định được các tính chất này giúp chúng ta hiểu rõ hơn về “hành vi” của hàm số trên từng khoảng xác định.
Vẽ đồ thị hàm số: Biến công thức thành hình ảnh trực quan
Tại sao chúng ta lại cần vẽ đồ thị hàm số? Đồ thị chính là “chân dung” của hàm số, giúp chúng ta:
- Hình dung trực quan: Thay vì nhìn vào công thức khô khan, đồ thị cho ta thấy rõ hình dáng, sự lên xuống, uốn lượn của hàm số.
- Nắm bắt nhanh các đặc điểm: Nhìn vào đồ thị, ta có thể dễ dàng nhận ra hàm số đồng biến, nghịch biến ở đâu, đâu là điểm cao nhất, thấp nhất (cực trị),…
- Giải phương trình, bất phương trình: Đồ thị giúp minh họa số nghiệm của phương trình (số giao điểm của các đồ thị) hoặc tập nghiệm của bất phương trình (phần đồ thị nằm trên/dưới một đường nào đó).
Các bước cơ bản để “phác họa chân dung” hàm số
Việc vẽ đồ thị thường bao gồm các bước (tùy độ phức tạp của hàm số):
- Tìm tập xác định: Biết “sân chơi” của hàm số.
- Xét sự biến thiên: Tìm đạo hàm, xét dấu đạo hàm để biết hàm số đồng biến, nghịch biến trên khoảng nào, tìm các điểm cực trị (nếu có).
- Tìm các giới hạn và tiệm cận (nếu có): Xem xét “hành vi” của hàm số khi x tiến đến vô cùng hoặc tiến đến các điểm không xác định. Đường tiệm cận giống như đường “biên” mà đồ thị sẽ tiến sát lại gần.
- Lập bảng biến thiên: Tổng hợp tất cả thông tin trên vào một cái bảng, giúp hình dung sơ bộ dáng điệu đồ thị.
- Tìm một vài điểm đặc biệt: Giao điểm với trục tung (cho x=0), giao điểm với trục hoành (cho y=0), các điểm cực trị,…
- Vẽ đồ thị: Dựa vào bảng biến thiên và các điểm đặc biệt, nối các điểm lại thành một đường cong (hoặc thẳng) mượt mà, thể hiện đúng dáng điệu đã phân tích.
Câu hỏi thường gặp: Vẽ đồ thị hàm số có khó không? -> Ban đầu có thể hơi lạ lẫm, nhưng khi bạn nắm vững các bước và luyện tập nhiều, việc vẽ đồ thị sẽ trở nên quen thuộc và dễ dàng hơn nhiều!
 Minh họa quá trình vẽ đồ thị hàm số
Minh họa quá trình vẽ đồ thị hàm số
Caption: Từ bảng biến thiên đến đồ thị trực quan – Hành trình “hiện hình” của hàm số.
“Khảo sát hàm số” – Thám tử toán học vào cuộc!
Nghe “khảo sát hàm số” có vẻ gì đó rất “hình sự” phải không? Thực chất, đây là một quy trình tổng hợp các bước phân tích (tìm TXĐ, xét sự biến thiên, tìm cực trị, giới hạn, tiệm cận, lập bảng biến thiên) và cuối cùng là vẽ đồ thị hàm số.
Mục tiêu của việc khảo sát là để hiểu toàn diện về một hàm số: nó bắt đầu từ đâu, kết thúc ở đâu, nó đi lên hay đi xuống ở những đoạn nào, đâu là đỉnh, đâu là đáy, hình dáng nó ra sao,… Giống như một thám tử thu thập đủ mọi manh mối để phác họa chân dung đầy đủ của đối tượng vậy!
Việc khảo sát và vẽ đồ thị hàm số là một trong những dạng toán trọng tâm trong chương trình phổ thông và cả ở bậc đại học, là nền tảng cho nhiều vấn đề toán học phức tạp hơn.
Hàm số không chỉ nằm trên giấy: Ứng dụng thực tế bất ngờ
Bạn có nghĩ hàm số chỉ là lý thuyết suông, chỉ để giải toán trong sách vở? Hoàn toàn không phải vậy! Hàm số có mặt ở khắp mọi nơi trong cuộc sống và các ngành khoa học:
- Khoa học và Kỹ thuật:
- Mô tả quỹ đạo chuyển động của vật thể (vật lý).
- Mô hình hóa sự tăng trưởng dân số, sự lây lan dịch bệnh (sinh học).
- Phân tích mạch điện (kỹ thuật điện).
- Mô tả các phản ứng hóa học (hóa học).
- Kinh tế và Tài chính:
- Dự báo xu hướng thị trường chứng khoán.
- Xây dựng mô hình cung – cầu.
- Tính toán lãi suất, lợi nhuận, tối ưu hóa chi phí.
- Công nghệ thông tin:
- Trong các thuật toán máy học (machine learning).
- Xử lý tín hiệu, đồ họa máy tính.
- Đời sống hàng ngày:
- Tính quãng đường dựa vào vận tốc và thời gian (y = v*t, một dạng hàm bậc nhất!).
- Tính cước điện thoại dựa trên thời gian gọi.
- Ngay cả việc điều chỉnh âm lượng trên điện thoại cũng là một dạng hàm số đấy!
 Ảnh ghép các ứng dụng thực tế của hàm số
Ảnh ghép các ứng dụng thực tế của hàm số
Caption: Hàm số hiện hữu trong mọi lĩnh vực, từ kinh tế, khoa học đến công nghệ.
Thấy chưa? Hàm số không hề xa vời mà vô cùng gần gũi và hữu ích phải không nào?
Làm thế nào để “chinh phục” hàm số?
Học hàm số có thể ban đầu hơi thử thách, nhưng hoàn toàn có thể “chinh phục” được nếu bạn có phương pháp đúng:
- Nắm vững lý thuyết gốc: Hiểu thật rõ định nghĩa hàm số là gì, tập xác định, tập giá trị. Đây là nền móng quan trọng nhất.
- Hiểu rõ từng loại hàm số: Nắm được đặc điểm, công thức, dạng đồ thị của các hàm số cơ bản (bậc nhất, bậc hai, mũ, logarit, lượng giác…).
- Luyện tập các dạng bài tập: Từ cơ bản đến nâng cao. Hãy bắt đầu với việc tìm tập xác định, tính giá trị hàm số, xét tính đơn điệu, tìm cực trị, rồi đến khảo sát và vẽ đồ thị hoàn chỉnh. Đừng ngại làm đi làm lại!
- Sử dụng công cụ hỗ trợ: Máy tính bỏ túi (để tính toán, kiểm tra kết quả), các phần mềm vẽ đồ thị online (như Desmos, GeoGebra) giúp bạn hình dung trực quan hơn. Nhưng nhớ là phải hiểu bản chất trước khi lạm dụng công cụ nhé!
- Liên hệ thực tế: Thử nghĩ xem các khái niệm hàm số bạn học có thể liên quan đến tình huống nào trong cuộc sống. Điều này giúp việc học bớt khô khan và ý nghĩa hơn.
- Đừng ngại hỏi: Nếu có bất cứ điều gì chưa hiểu, hãy mạnh dạn hỏi thầy cô, bạn bè hoặc tìm kiếm các nguồn tài liệu đáng tin cậy (như Tailieusieucap.com chẳng hạn 😉).
Quan trọng nhất: Hãy kiên trì và giữ thái độ tích cực. Ai cũng cần thời gian để làm quen và thành thạo một kiến thức mới.
Ý nghĩa của việc học hàm số
Việc nắm vững kiến thức về hàm số mang lại cho bạn rất nhiều lợi ích:
- Kiến thức nền tảng: Là chìa khóa để học tốt các phần khác của giải tích (đạo hàm, tích phân) và nhiều môn khoa học khác.
- Tư duy logic và trừu tượng: Rèn luyện khả năng phân tích, suy luận, nhìn nhận mối quan hệ giữa các yếu tố.
- Kỹ năng giải quyết vấn đề: Áp dụng kiến thức hàm số để mô hình hóa và giải quyết các bài toán thực tế.
- Mở rộng cơ hội: Kiến thức vững chắc về hàm số là lợi thế lớn khi học lên cao hoặc theo đuổi các ngành nghề liên quan đến khoa học, kỹ thuật, kinh tế, công nghệ.
Kết luận
Vậy là chúng ta đã cùng nhau đi một vòng khám phá thế giới đầy màu sắc của hàm số. Từ những định nghĩa cơ bản, các loại hàm số đa dạng, cách vẽ đồ thị, khảo sát cho đến những ứng dụng thiết thực trong cuộc sống. Hy vọng rằng, qua bài viết này, hàm số không còn là một khái niệm “đáng sợ” mà đã trở nên gần gũi, dễ hiểu và thú vị hơn với bạn.
Hãy nhớ rằng, hàm số là một công cụ vô cùng mạnh mẽ để mô tả và hiểu thế giới xung quanh chúng ta. Đừng ngần ngại đầu tư thời gian để tìm hiểu và luyện tập. Sự kiên trì của bạn hôm nay sẽ mở ra những cánh cửa tri thức mới trong tương lai!
Bạn thấy bài viết này thế nào? Bạn còn thắc mắc gì về hàm số không? Hãy để lại bình luận bên dưới nhé! Và đừng quên chia sẻ bài viết này nếu bạn thấy nó hữu ích. Tailieusieucap.com còn rất nhiều bài viết hay và tài liệu chất lượng khác đang chờ bạn khám phá đấy!
[internal_links]
- Khám phá thêm về Đạo hàm – Người bạn đồng hành của Hàm số
- Tuyển tập bài tập Hàm số có lời giải chi tiết
- Các phần mềm vẽ đồ thị hàm số tốt nhất hiện nay
Chúc bạn học tốt và luôn tìm thấy niềm vui trong Toán học!